Quick tips

• to transform frames, you need the Homogeneous transformation (it is not sufficient to do a rotation)

Notation Introduction

The important notation choice is how we represent a frame of reference. We use the pre-superscript to denote the origin, i.e. $^AP$ represents some point defined in terms of frame $A$. Always, the pre-superscript shows us how something is defined. Use a pre-subscript to reference the represented frame.

• $^AX_B$: some vector $X_B$ (the x-direction unit vector) as defined in frame $A$

• $^A_BR$: orientation of frame $B$ with respect to $A$’s coordinates

• $OP$ is a vector that points from the origin to a point in space, $P$.

• We generally use $P$ to reference a point. If this point happens to be a frame, you use a normal subscript. So $P_B$ would be the point of frame $B$, and $^AP_B$ would be the representation of frame $B$ in $A$.

• We may also use the format $P_{A/B}$ to indicate that this is the position of a point $A$ in FOV $B$

Manipulator Structure

Let’s try to formalize the definition of a robot manipulator and the different definitions. A manipulator has a number of rigid body links connected through joints. The last part (the manipulator) interacts with the environment, known as the end-effector. The first part is connected to some solid surface and is known as the base.

By simple calculations, manipulators have $n$ joints and $n+1$ links. Because one of them is fixed, there are $n$ moving joints.

Joints

We assume that the joints only have one degree of freedom. This yields two possible joint types.

• Prismatic joints will create linear motion

• revolute joints will create rotational motion

Joints have limits that must be respected.

Generalized Coordinates / Joint Coordinates

Degrees of freedom

Each mobile link can be described by 6 parameters: 3 for position and 3 for orientation (like euler angle). Therefore, we say that the link has 6 degrees of freedom. Therefore, the links can be described by $6n$ total parameters.

However, each joint only affords a single degree of freedom relative to the previous joint. So, 5 out of the 6 parameters per link is actually redundant. As such, the total degrees of freedom of a manipulator is $6n - 5n = n$. Or, in other words, each segment adds a single degree of freedom.

Creating joint coordinates

The discussion on degrees of freedom leads us in the direction of deriving a concise set of coordinates that can represent the entire system uniquely. The number of coordinates is the same as the DOF, which should make intuitive sense.

You end up having this joint space where each axis is a joint angle (or linear actuation depth), and each point is therefore a robot state.

Operational Coordinates

Instead of describing the positions of all the joints, we may also just try to describe the position and orientation of the end-effector. Now, if there are enough degrees of freedom in the robot, this EEF will have all six degrees of freedom. However, if we are less fortunate, this end-effector may not have all six.

We can plot the operational space very similarly to the joint space, but each axis comprises a degree of freedom of the end-effector

Redundancy

If the number of joints is greater than the maximum degree of freedom of the end-effector (typically six), we say that the robot is redundant. The degree of redundancy is the number of additional degrees of freedom.

As a brief hint of what’s to come, notice that operational coordinates may not map 1:1 to joint coordinates if there is redundancy.

Representing Rigid Bodies

One big lesson is to consider points / vectors as different than their representations. Point and vectors and, well, everything, can exist without numbers. However, as soon as you’re trying to represent them, you run into the need for references. That’s where the math comes in.

What’s agnostic to representation?

This is repeating some material but it’s important, so it’s worth it. Certain things are agnostic to representation, some of the time. In fact, everything is technically agnostic to representation until we want to talk about it (this is almost a philosophical point). Operationally, let’s start with points. These are agnostic, and therefore vectors defined by these points are agnostic, and therefore whole frames are also agnostic.

Therefore, certain operations are agnostic to representation, like vector operations, etc.

However, in this state, we can’t really represent these things. Implicitly, points need to be defined in terms of an origin, and vectors as well. Therefore, the second we want to talk about them, we need to define such an origin, and this is where the pre-superscript and pre-subscript notation come from. This is also where the rotation matrices gain some meaning, etc. This is a very nuanced point…maybe it will become more clear as we become acquainted with the notation and the subject.

Vectors

If we have a reference point $O$, any point in space can be denoted as the vector $p = OP$. Now, here’s some nuance: the vector $p$ exists without any reference point; its something that points somewhere. To get the point $P$, you need to define where it starts: the reference $O$.

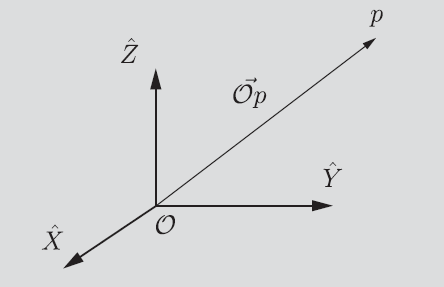
However, the components of $p$ is not agnostic to the reference point (rotate the origin and all the components change). The components are defined in terms of $O$’s unit vectors.

So, to put this concisely: $p$ is a direction, and these directions are agnostic to points of reference. If you are only dealing with vectors, there’s no need to specify a frame of reference. The upshot is that you can perform operations like dot products without worrying about the origin, as long as the two vectors share the same origin.

However, the representation of the vector is sensitive to the point of reference. Because we often do care about the components, we will typically use the notation $^Ap$ to specify the frame.

Looking at a rigid object

If you think about it, a rigid object is just another frame of reference. You can describe this second frame of reference in terms of your original frame of reference. The second FOR needs a center point (the $^Ap$ described above), and then a rotation. We figured out how to talk about position, but what about orientation?

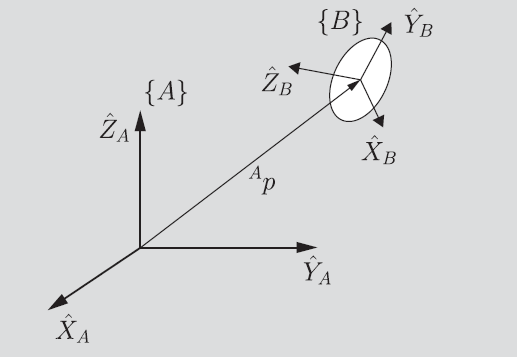
Rotation Matrix

We denote $^A_BR$ as the rotation matrix that tells us the orientation of frame $\{B\}$ with respect to $\{A\}$. Mechanically, $^A_B R$ represents the three unit vectors of $\{B\}$ as seen in $\{A\}$.

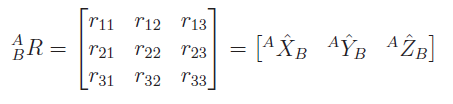
The rotation matrix is orthonormal, which means that the transpose is the inverse:

Here’s a good interpretation

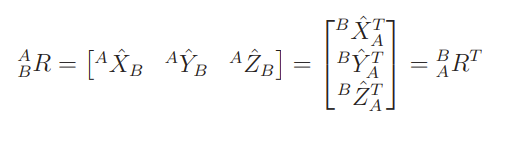
We are expressing the orientation of $B$ in $A$, which is why the columns are in $A$ frame. The rows, therefore, must go the other way. Each row must express the orientation of $A$ in $B$.

What is a valid rotation matrix?

A rotation matrix must be a rigid, non-inverting transformation. Therefore, these are necessary

• $det(R) = 1$ (not negative 1)

• $R^T = R^{-1}$, i.e. $R^TR = I$

Changing Descriptions using Rotation Matrix

If we have anything in $B$, we can easily get it into $A$ by computing

Because $^BP$ is in terms of the $B$, and $^A_B R$ tells us how to take each unit vector and move into $A$.

It follows, therefore, that you can chain rotations together, because each rotation is just a collection of column vectors:

Rotation Matrices as Projections

As you think back to linear algebra, we note that this $^A\hat{X}_B$ and the other two are just projections of the unit vectors of $\{B\}$ onto the unit vectors of $\{A\}$. As such, this vector can be written as dot products.

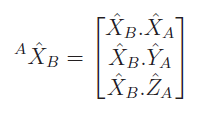
Note how we don’t care about the reference points of the $\hat{X}_B, \hat{X}_A$ because they are just vectors and we only care about the dot product.

The whole rotation matrix can therefore be expressed as projections

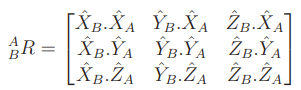
Transforms

Previously, we talked about how to represent positions and orientations with respect to some base. Now, let’s talk about how we can take some representation and move it into another basis. That’s what we call a transformation.

Pure translation

Say we had some point $p$ and we know its representation with respect to $O_B$, an origin. Suppose that we also knew the vector $P_{AB} = O_A → O_B$. From this, you can derive that

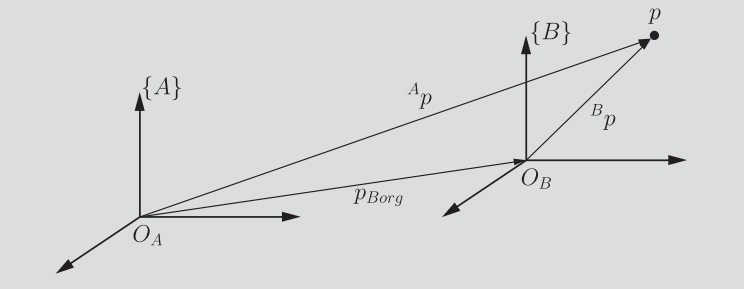
This should feel like a “duh” moment, but we are trying to be rigorous such that adding rotations won’t feel like a huge jump.

General Transformation

A general translation is a combination of a rotation and a translation. Let’s discuss this using our two interpretations

• Frame shift: you have a point in $B$. To get it to the base $A$, we first have to align this base $B$ with $A$, and then perform a pure translation.

• Physical motion: You have something at $A$. You move it to $B$ (pure translation), and then you align it with the reference $B$ (pure rotation)

The general transformation equation, therefore, is a composition of a rotation and a translation. It helps to rotate first into $A$’s orientation because then we can use the vector displacement in $A$.

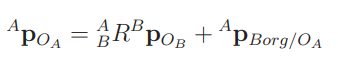
If you were to translate then rotate, then you would need to find $^Bp_{Borg/O_A}$, which is fine. Transformations and rotations are commutative (compositions of rotations, however, are not. But we’ll get to those later).

Homogenous Transform

Matrix representation of a general transformation

Because this general transformation can be a little intimidating, it’s also possible to create a shorthand that does it all in one step. The shorthand takes the place of a 4x4 matrix:

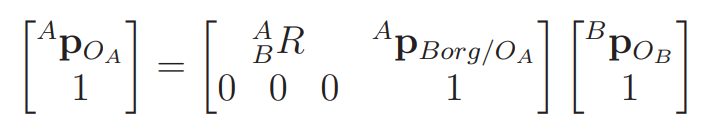
You feed in a representation WRT $B$, multiply by the matrix, and you’ll get the same point WRT $A$.

Three interpretations of homogenous transformation

As such, there are three ways of interpreting a homogenous transform

1. Frame description: The $^A_BT$ fully represents a frame $B$ with respect to a base $A$.

2. Transform mapping: $^A_BT$ will map B→A

3. Transform operator: the same $^A_BT$ represents the motion from A→B, which means that we can apply this transformation to any points or vectors, etc.

Transforms as Operators

A transformation can be interpreted as a mapping from $B → A$, but it can also be interpreted as an operator (physical motion). Let’s flesh this out a little bit.

• Mappings are always static—they deal with the same points and map between different frames of reference

• Operators are dynamic—they deal with moving some point within the same frames of reference

Building up intuition

Let’s flesh out a critical duality of all transformations. A transformation can serve two purposes: $_A^BT$ can…

1. Map a point in space $A$ to space $B$. In this case, nothing is moved, but the reference is changed.

2. Imagine moving frame $B\rightarrow A$ and carrying some vector $v$ with this rigid transformation. This is the operator definition.

Note that the operator definition doesn’t need any frame of reference; it refers to a general motion that is agnostic to reference. So an operator doesn’t have a reference point.

So any composition of transforms has two ways of interpreting it:

• Right to left: the operator interpretation. You’re imagining three motions that move from $D→B, C→D, A→C$ and applying them consecutively

• Left to right: You’re moving a world frame from $A→C, C→ D, D→B$. Ultimately, this gives you a motion from $A → B$, which can be used to define $_B^AT$. Note how this isn’t an operator definition; you can’t think about what a vector would do in this circumstance.

Rotations

A rotation matrix around the target axis would move the other two axes, of the form

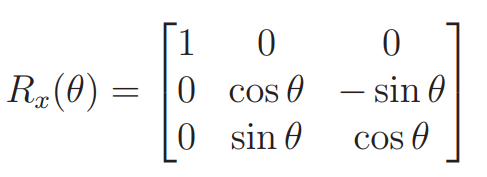
To reinforce our prior insight, let’s have the base be $A$ and this rotated space is $B$, and the thing above is $^B_AR$. This is a physical action that impacts the whole world. So any vector is impacted, and you can do matrix multiplication of any vector to get the transformed vector. Again, it’s worth noting that because we don’t use the origin here, it doesn’t matter that we start with a vector in reference point $A$.

Homogenous Operators

As before, we can represent a homogenous translation + rotation as one matrix, and this can be interpreted as a single matrix multiplication that moves $p_1$.

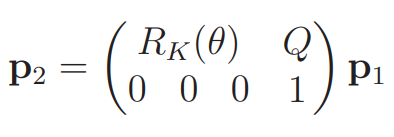
Inverse Transforms

We saw previously that we can invert a rotation very easily. We can also invert a pure translation very easily (just negate the vector!). But what about a homogenous transformation? Well, the homogenous matrix isn’t orthonormal at all, so we can’t just take the transpose.

Turns out, if we have a homogenous transformation

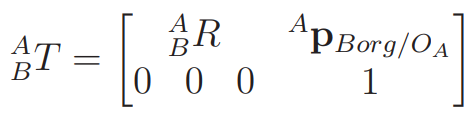
we can express the inverse transform as the following:

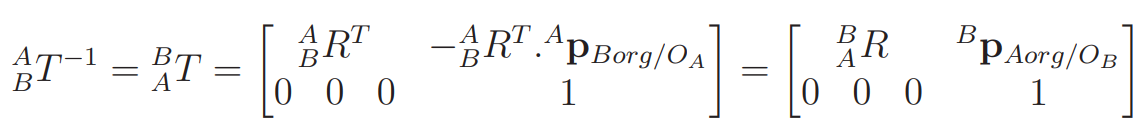
If you think about this, it actually makes a ton of sense. To show $B$ in base $A$, we needed everything in the matrix to be in $A$. To reverse the process and show $A$ in base $B$, we need everything in the matrix to be in $B$. That’s easy for the rotation (transpose), but for the displacement, we need to first convert to frame $B$. Then, we can negate.

Composition of Transforms

Here’s a general rule of thumb: math always operates right to left, but you can imagine going from left to right. Consider this chain:

This can be interpreted as expressing $x$ in terms of $D\rightarrow C → A →B$, or you can think of transforming from $B → A → C→D$.