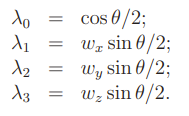The importance of orientation representations

In the previous section, we talked about one way of representing orientations: through a rotation matrix. While that is still going to be the main way of representing a rotation, there are other ways of rotation representation that are important.

Direction Cosines & Rotation Matrix

The rotation matrix contains 9 elements, but there aren’t 9 degrees of freedom. In fact, there are only three. The elements of the matrix are related to each other through orthonormality, which imposes 6 constraints, meaning that there is only 9-6 = 3 degrees of freedom.

We can flatten the matrix into a 9x1 vector, which is called the direction cosines.

Rotation matrices of simple rotations

For future reference, here are the rotation matrices that correspond to the simple axis rotations. Note that the Y axis is slightly tricky!

Note how the sines are swapped; if you’re confused, just draw the vectors as they rotate

Euler and Fixed Angle

A common way of representing rotations is through a series of elementary operations, like three rotations around different axes.

Euler Angles

The euler angle is defined as a set of three rotations, made around the axes of the transformed frame. You can understand this as a composition of elementary rotation matrices:

Because we are talking about a transformation, you read the order from left to right. So we would call this particular euler angle as a ZYX ordering. There are 12 types of euler angles, because there are 3 choices for the first axis, and 2 choices for the remaining 2 (we can repeat rotations as long as they are not consecutive).

Each of the elementary rotations are easily represented by a rotation matrix. Because matrices typically don’t commute, the ordering of transformation is critical.

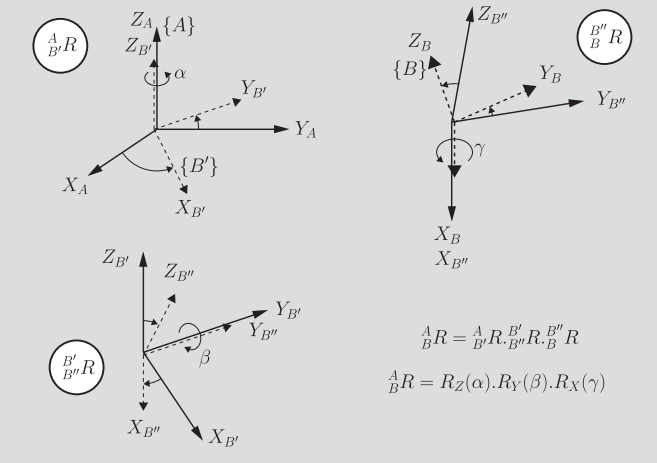
Fixed Angles

Fixed angles are also a composition of rotations, but instead of using the transformed frame, we use the origin frame. You might think that this is complicated (as you can no longer just compose rotations), it’s actually surprisingly elegant.

If you imagine some vector going through a fixed angle transformation, you’ll just compose the rotations in the order you read them off. So for an XYZ transformation, you’ll have

Euler vs fixed

And note that this is exactly the same as the $_B^AR$ in the euler angle with the ZYX ordering. This is an important duality.

• Left to right: you’re moving a coordinate system through these transformations

• Right to left: you’re applying fixed-angle transformations to a vector

They are the same things, just two different directions of reading. So euler and fixed angles have the same angle and the same decomposition; you just read the angles in reversed order

Notationally, you write things in opposite ways:

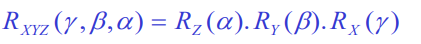
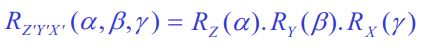
Finding the angles

If we are given a rotation matrix $R$, can we find the euler / fixed angles? Yes! For a ZYX euler angle, we have

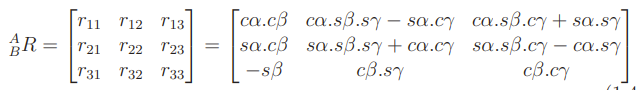
You can solve for $\alpha, \beta, \gamma$. You should start by finding $\cos \beta$ and $\sin \beta$. Then, you can start solving for more of the parameters—it is just algebra at this point.

While solving for $\beta$, you can write

This will get you a solution(s) for $\beta$, which you can then use to solve for $\gamma$ and $\alpha$ through this formula

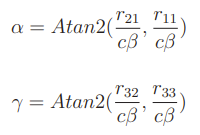
There can be some interesting singularities that arise from this formulation. If both $r_{11}, r_{21}$ are zero, we reach a problem where $\beta$ actually has no solution. You run into the issue of $\cos \beta = 0$. If this is the case, then one of the vectors must be an unrotated vector. Furthermore, this means that we can’t determine $\alpha, \gamma$ directly anymore. We can only derive their relative differences

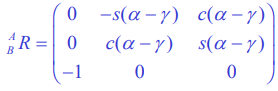
This means that two rotations have been collapsed into one. This means that the overall rotation matrix is the composition of only two rotations.

What does this mean in real life? Well, it means that you may not be able to hit all orientations using the euler approach.

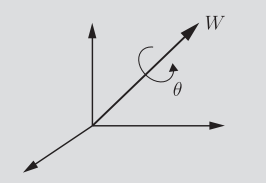
Angle Axis representation

Any rotation can be represented as a rotation around some axis with angle $\theta$.

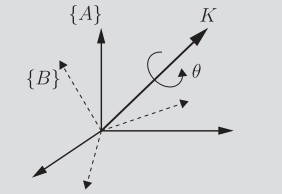
Which means that you can represent this rotation as $\theta k$, where $k$ is the unit vector and $\theta$ is the angle. You can solve for $k, \theta$ using this formula

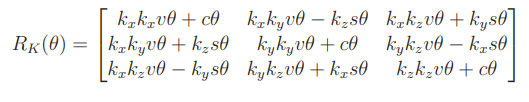
where $v\theta = 1-c\theta$.

If you work it out, you’ll get that

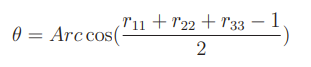
and

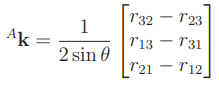
Notice how there is a singularity if $\sin \theta = 0$, which can happen at $0, 180$.

Quaternion

As we saw, both euler angles and angle-axis representations suffer from singularities. This is an unfortunate truth about rotation representations. We need an extra redundant dimension.

The euler parameters, or Quaternion, provides a unit vector $w$ and a rotation of angle $\theta$. So it’s very similar to Axis Angle but it’s encoded in a more tricky way.

and the norm of the parameters is 1, for obvious reasons. But this is quite interesting, because the vector of $\lambda$ is in a unit hypersphere and it can cover the whole hypersphere. However, the hypersphere is redundant; half of it represents the same rotation.

Inverse

Given quaternion parameters, we can derive the rotation matrix as follows

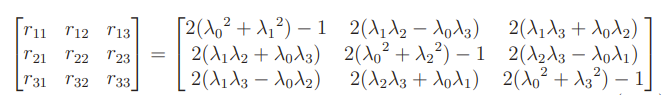
To compute the inverse, you should start at $\lambda_0$ by looking at the sum of the diagonal elements. Because of the redundancy, you only need to worry about one of the roots of $\lambda_0^2$.

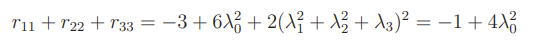
And you can compute the rest

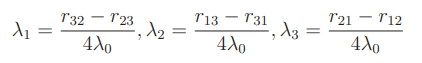
If $\lambda_0 = 0$, then start with another parameter. They can all be computed relatively easily. You will always be able to find a euler parameter that is greater than or equal to $1/2$.

You can also convert from ZYX euler angles to quaternions using the following:

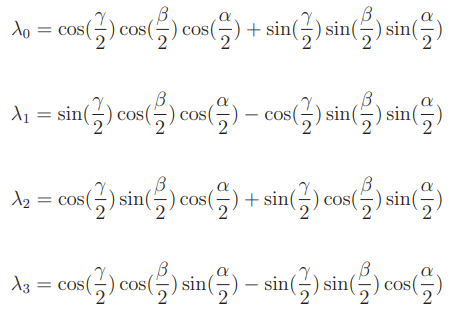
Deeper mathematical connection

This is a bit beyond the paygrade, but a quaternion also represents a numerical system with three imaginary components and one real component. There are some neat properties because of this numbering system that I won’t get that much into right now.