What is inverse kinematics?

When we want a particular pose and orientation in the end-effector, we beg the question: what angles and offsets do we need to hit that goal? And is it even possible?

At a glance, we understand this to be a hard problem. In many cases, there may be multiple solutions. In the diagram below, position $B$ has two solutions

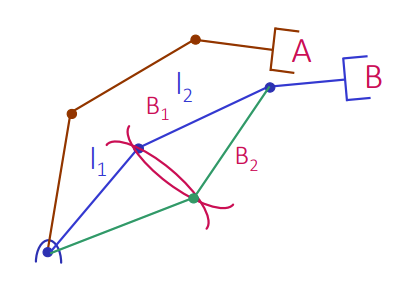
We might want to pick $B_1$ if we are getting from position $A$ to $B$, because it requires less movement.

In other cases, there may be no solution. The joint space and the pose space are related through a series of convoluted sines and cosines.

Closed form solutions

In very simple cases, it may be possible to solve for the inverse function. There are two types of solutions: algebraic and geometric solutions.

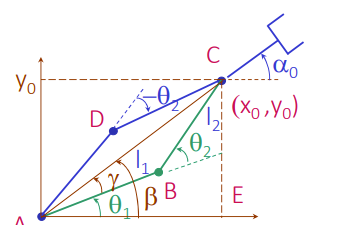
Geometric solutions

The idea here is just to look at the different angles and apply geometric tricks to derive the angles.

Algebraic solution

The algebraic solution looks more at the transformation matrix and we just try to solve the end-effector transformation in terms of joint angles.

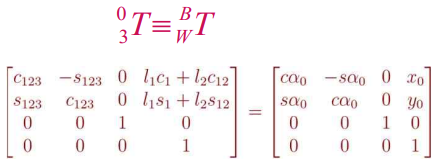
The key lesson of the day is this: it’s very hard to find a closed-form solution if the system is not simple.

Closed-form Pieper’s solution

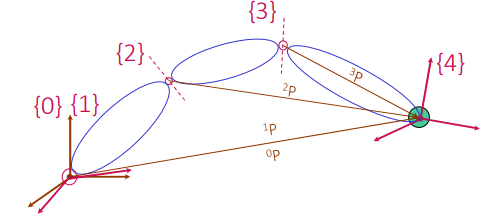
There is a special case where we have three joints and then three more joints that are overlapped. In this case, we can use Pieper's solution to solve explicitly for a closed-form expression.

This works because the position depends on three angles only, and the rest are solved separately. This reduces down into a 4th degree polynomial.

Workspace

The workspace of a robot is the places in task space that it can reach. You can interpret this as the range of the forward kinematics function.

There are two types of workspaces: reachable workspace are the set of points that can be reached. The dextrous workspace is a stronger condition that is the set of points that can be reached for all possible end-effector orientation (allowing manipulation, etc). It is a subset of the reachable workspace.

Mathematically, a reachable workspace you only care about the displacement vector in $T$. A dexterous workspace you care that a point is reachable as well as possible to reach all possible rotation matrix values.

Calculating workspace

This can be a bit tricky; it requires an amount of spatial reasoning. Imagine each joint defining a plane. Start at the end-effector and work your way back. Each joint will “sweep” the shape that is the workspace of the joints in front of it. This might yield a complicated shape.