Forces and Acceleration

Tags	Dynamics

Development of forces

Jacobians can actually tells us the relationship between forces at the end-effector and the torques at the joints. But we will show this slowly. First, let’s talk about forces. The moment, or the torque $N$ is defined as the cross product

N = p\times F

where $p$ is the radius and $F$ is the applied force.

Summing moments

Much like angular velocities, moments are vectors that are agnostic to position. In other words, you can have torque being applied to different points, but you can add these points together to get the total moment.

Force Propagation

Force propagation is similar to position or velocity propagation because you’re essentially starting with what you know, and you end up deriving the torques sequentially. However, (and this is pretty neat because of duality), instead of the base, you start at the end-effector. This is because you know the forces on the end-effector, and you know that they have to be balanced. More on this in a second.

Single Link

Right now, we care about static forces, which are forces that occur when the robot is standing still. Now, for this to happen, the sum of forces and moments must be both zero.

Let’s focus on a single link

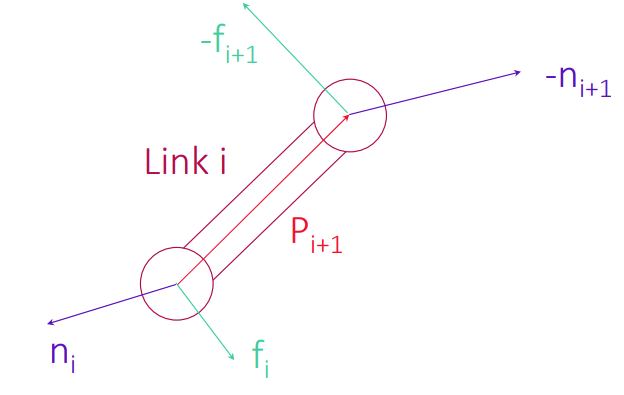
You compute the moment and the force at each joint. From this, you get two critical equalities

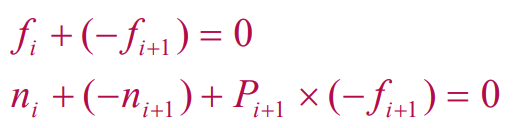
The first equality comes from force, and the second equality comes from the definition of moments.

Propagating the forces

You start at the very end of the EEF and figure out what force it’s trying to exert. Then, you can get the equal and opposite force that is being exerted on the arm. This is the force you start with (denoted as $-f$ on the arm).

Good rule of thumb: the end of the link has some force that is being exerted on it, denoted as $-f$ . This is directly from the next joint’s $f$ and it not subject to chnage (newton’s third law). From this you derive your next force and torque.

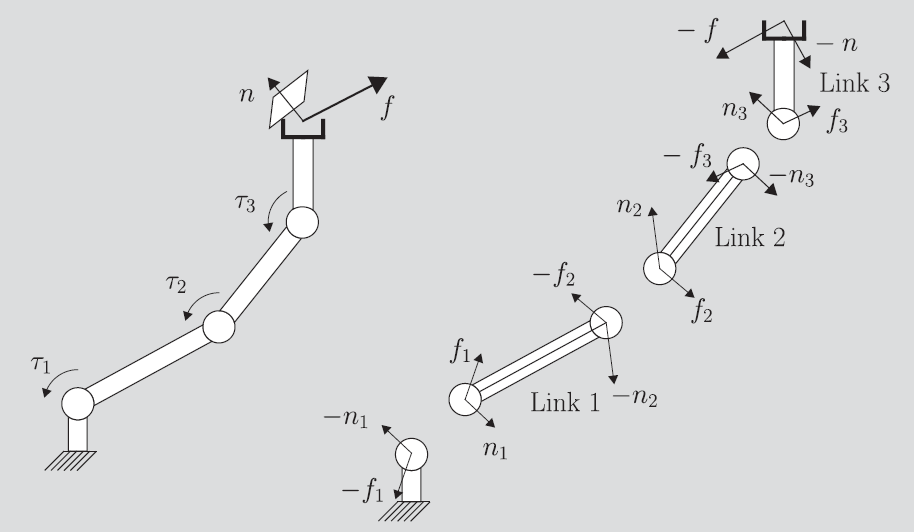
Intuitively, if you imagine supergluing the joints and not caring about the joint torques or forces, this robot is just an elaborate stick. This stick will transmit force directly. If you are in static land, the robot should act like a stick to the outside observer. Now, to maintain this stick-like rigidity, you need to apply certain torques on the joints.

The torques are not just equal and opposite because the forces exert additional torques on the joints, so those have to be factored in.

Finding the actual joint forces / torques

But here’s the interesting question: there’s a lot of forces going through the robot, but only some forces matter. The forces that matter are the ones that exert an explicit torque on the robot joints or an explicit force on the prismatic joints.

For this, we just need to project the exerted force or torque onto the axis $z_i$ of the robot. For a prismatic joint, we have

\tau_i = f_i^TZ_i

and for a revolute joint, we have

\tau_i = n_i^TZ

Virtual Work

So the whole thing we described above with force propagation and then projection is actually kinda annoying. We can’t see anything elegant about it. But what if we use an energy argument? More specifically, there should be no net work done on the robot arm if we are stationary. This equation is

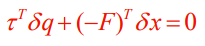
And because we know that $\delta x = J\delta q$ , we get

\tau^T \delta q = F^T J\delta q

which gives us the relationship

\tau^T = F^T J

And therefore,

\tau = J^TF

💡

THIS IS THE CRITICAL RESULT: to compute the torques on the robot, all you need to do is compute the Jacobian and then transpose it! Intuitively, this jives with propagating the forces backwards.

Unpacking this $J^TF$ relationship

This is something that you get for $J_w$ as well as $J_v$ . You can compute this independently. Let’s consider the $J_v$ for a second. It allows you to represent each joint torque as a function $F_x, F_y, F_z$

Each $F$ component is the force that the robot can apply. There can be vectors of $F$ in the nullspace of $J^T$ , which means that there is no value of $\tau$ that yields this $F$ . Simply put, this force is impossible for the robot to apply.

This can be a bit confusing, because $J^TF$ actually yields the zero vector if $F$ is in the nullspace. To help with this interpretation, imagine that the robot is reacting to an applied force. Because this force is impossible to exert, it means that all the force is going through the structure. So the robot wouldn’t need any torque or force to support this applied force.

So how does this jive with the first interpretation? Well, remember that every force has an equal and opposite reaction. So when the robot is trying to apply force, it must also react to the force that it’s applying. A robot can apply a force if it can react to the opposite force with an $F$ with no components in the nullspace of $J^T$ . If there are any components in the nullspace, then the robot can’t exert that force; it can only support it.

Another thing to note: support means that the force is being directly applied to the robot. This is actually $-F$ , because it’s external. Applying force is $F$ .