The Numbers
| Tags | MATH 115 |
|---|
What is analysis?
Analysis is the breakdown of calculus and the rigorous buildup of each subject. We start by the definitions of certain spaces and symbols (here), then we build up to sequences, continuity, differentiation, and finally integration. At times, it will feel backward, because we know everything that will be proven in this course. But that’s kinda fun!
PROOF TIPS 🔨
- Infimums and supremums: use the definitions. Propose some to perturb the defintions, etc.
- Dedekind cuts: when you’re dealing with , look at subsets and make element-arguments.
- for contradictions; follow one definition and ignore perhaps another conflicting definition. You will eventually reach a contradiction with this other defintion.
Natural Numbers
The set of natural numbers is just the set of positive integers, with a special successor. For every , let .
Peano Axioms 🐧
-
- if , then
- is not the successor of any element in
- If , then
- If and
-
- if
- then,
Now, these axioms are showing a test about a set and a successor definition. It happens that and satisfy these axioms. But you can easily define other sets that work too. For example, let and let . This works!
Peano and Induction 🚀
We can show that the fifth statement actually shows the basis of matematical induction.
Let be statements that may or may not be true. Let be the set of all true statements. With induction, we need to show that
-
- if
And by the fifth peano axiom, if we have shown this, then we have shown that all is true.
Formal definition of addition 🐧
We want to define , and we do this inductively. We start with the base case of , which is just .
Now, we move to the inductive case. Given , we want to see what is.
which completes the induction
Here, we define the associative property, which allows us to inductively define addition. Without the associative property, there is no addition.
Formal definition of multiplication 🐧
We want to define inductively. The base case is , which is just . Inductively, we assume that we have . We want to see what is.
which completes the induction, with help from our formal definition of addition.
Here, we define the distributive property. without the distribution property, there is no multiplication
Formal definition of order 🐧
Similarly, we want to define what it means to have and so on. We do this through two stages of induction. First, as the base case, we set . Now, we show in an inner induction that $$1 < b for all .
In this base case, we have , which is true. For the inductive step, we are given and want to show that . We can expand to get , which gets us , and because we have established that (I think) and we use the transitive property, we are done with this induction. Again, like addition and multiplication, we notice that transitivity is necessary for the definition of order.
Now, for the rest of the induction, we just need to do the same inductive step as above, but with generically. The same steps hold.
Minimal Principle 🚀
If and is not an empty set, then has a minimal element.
Proof
By contradiction. Let’s say that is a non-empty subset without a minimal element. Let , where the subtraction denotes a set operation.
must contain 1, because 1 is the smallest natural number and if contained it, then it would have a minimal element.
Now, let’s look at it inductively. Assume that contains all numbers up to . We claim that contains all numbers up to , because if we were to put in , then this number would be the minimal element. Therefore, we conclude that all natural numbers belong to and is the empty set. This is a contradiction, and we are done.
Integers
Moving from natural numbers 🐧
We’ve shown addition on the natural numbers. But we are left unsatisfied, because it is possible to have some such that . This motivates the need for . This general strategy is something we will use to develop the whole number system. We start at one place, and find that we can construct something else with what we have.
The symbol is the set of integers, which can also be expressed as
With , we have addition, multiplication, subtraction, and ordering. These can be proved in a similar way.
Modified minimal principle 🐧
Any finite set of does have a minimal element, but we can’t say that this is the case for all sets. For infinite sets, we can say the following:
Let be a lower bound on the set . We can perform a bijection on this set to by setting
This brings us into the realm of natural numbers. Now, we can safely apply the minimal principle.
So the tl;dr is that the following are necessary and sufficient conditions to have a minimum
- set is finite
- set has a lower bound
If the set is infinite and lower bounded, you end up with an infimum.
Rational Numbers
Moving from integers 🐧
Similarly to how we motivated , we see that equations of where may yield an . This requires the development of .
The symbol represents the set of rational numbers such that . There are a ton of rational numbers (in fact, infinitely many of the same cardinality of ), but there are still gaps.
Modified minimal principle 🐧
Like before, any finite set does have a minimal element. However, unlike , having a lower bound on a set does NOT guarentee that there is a smallest element. For example, we can define
The lower bound here is , but there are an infinite number of elements in the set , with none of them being the smallest. You can always propose something smaller.
Therefore, in , we encounter some weirdness. We can define lower bounds, but this doesn’t necessarily translate to having a smallest element in the set.
Infimum and supremum ⭐🐧
The infimum is the greatest lower bound. This is formally with two necessary and sufficient terms
- for all , . This establishes the lower bound part
- If there exists some , then there exists some such that . This establishes the greatest lower bound part.
The supremum is the lowest upper bound. There are two very similar necessary and sufficient terms
- for all , . This establishes the upper bound part
- If there exists some , then there exists some such that . This establishes the lowest upper bound part.
Here’s an important thing to note: all minimums are infimums, and all infimums are lower bounds. All maximums are supremums, and all supremums are upper bounds. We are going from tight to loose to looser.
In subsets of N and Z, either infimums/supremums don’t exist, or they are equal to maximum/minimum. In subsets of Q, it may not be another element from the set. It may not even be another element from Q itself. This fact is actually critical for establishing R, which we will do in a later section.
Proving irrationality in general 🔨
Typically, if something is irrational, we can prove by contradiction. Let be equal to the number in question and solve for and .
Classical example
Prove that is irrational.
by contradiction
- Assume that exists where are coprimes
- .
- Therefore, is even, meaning that is also even. But if is even, it must have at least a factor of , or else the square doesn’t make sense
- We are only given one factor of on the RHS, so the must have at least a factor of , which makes even as well.
- both are even, so they share a common factor of . This is a contradiction.
Proving irrationality through rational zeros theorem 🔨
We define a number an algebraic number if when you plug it into a polynomial , it yields 0, where all are integers.
Rational numbers are always algebraic numbers, because if , then we can set up with that solution. However, not all algebraic numbers are rational, because it includes irrational square roots, etc.
Given a polynomial
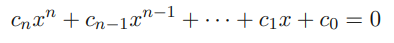
if , a rational number that satisfies the equation, then divides and divides .
Proof
It’s actually just simple algebra. Let’s start in a good place: plugging what we know in
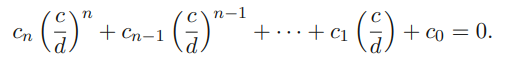
We multiply through by and get

Now, let’s solve for . Note how we can factor out
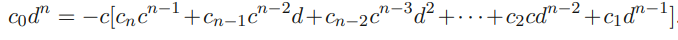
because and share no common factors, this statement can only be true if divides , as desired.
Now, let’s solve for . Here, we see that we can factor out a , and using the same logic as above, we claim that the statement is only true if divides , as desired.
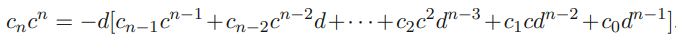
This means all rational roots must satisfy the above constraints. Therefore, you can actually enumerate out the rational roots and find all of them easily.
And therefore, we stumble upon another way of proving rationality. Every algebraic number can be expressed as a polynomial (set equal to the expression, and square/cube, etc stuff until it’s integers). Find all the rational solutions using the rational zeros theorem and enumerate. If none of them yield a zero, then you say that none of the roots are rational, and therefore the original number, which was a root, can’t possibly be rational.
Pro tips
- all coefficients must be integers. If you are left with a root of some sort, isolate it on one side, raise it to the inverse power, and expand. Keep on doing this until you are left with just integers
Real Numbers
One thing we note is that we can define some set such that . An easy example is
which has . This shows us that is incomplete, and it also gives us an idea for how to “fill in” those gaps through the infimum definition
Dedekind cuts 🐧
A dedekind cut is a pair of subsets such that
-
-
-
- for any
- has no maximal element, and has no minimal element (although you might have a minimal element if is defined to have a minimal element…)
Graphically this looks like a number line with a singular cut in it.
The key insight here is that we can use Dedekind cuts to establish numbers! Notationally, we usually say that where the () represents the cut.
We observed in the previous section that infimums of rational element sets don’t necessarily belong to Q. The Dedekind cuts exploits this to make the jump from Q to R, as we alluded to before. In fact, we now define the real numbers R as the set of possible Dedekind cuts with constraints in Q.
Properties of Dedekind cuts 🚀
Toy examples
We can define by letting . Note that doesn’t have a maximal element here, like stated.
We can define any rational element through the exact same way; just replace with .
- The number represented by is the supremum, which means that it may or may not be in depending on the circumstances
Laws of addition & multiplication 🐧
Like before, we must establish simple laws in our new system of Dedekind cuts. Addition is pretty straightforward. If we have , we have Dedekind cuts . We want to formulate a dedekind cut , that corresponds to .
As it turns out, we can just do this
which means that
Because we were able to form a Dedekind cut that represents , we are done. Now, to show that this is a valid cut, you would need to show that the Dedekind cut properties actually hold, but let’s just assume that we can do that.
You can also define multiplication in a similar pairwise way.
Laws of ordering 🐧
We can also define ordering in terms of Dedekind cuts in actually a really elegant way
- iff and vice versa
- iff .
This should make sense pictorially.
Density of rational numbers in R 🚀⭐
Theorem: for all , there exists some such that .
Proof
The proof hinges on the fact that we can construct Dedekind cuts with subsets of
if we have , then . This middle point is arbitrary but it helps us a avoid an edge case.
Therefore, the cut , which means that there is some that is not in , which means that it is less than , and it could be equal to because the cut may or may not include the edge. This means that , and because it is rational.
Upshot: even though there are holes in Q, the set of rational numbers is dense in R. This is where it becomes funky, just because the concept of infinity is weird to us.
We can also show something stronger: there exists an infinite number of between any pair of real numbers. You can do this by finding two in (just split the inteval in half and use the previous theorem to get the two , and from these two , you can make an infinite number of rational numbers
The completeness Axiom ⭐🚀
This is the most important result here. We show that doesn’t lack anything (i.e. no holes), unlike all other number system. We do this by showing that all subsets of with a lower bound have an infimum (naturally in ).
Why does this show completeness? Well, suppose that we constructed a Dedekind cut, but this time, it’s across , i.e. . Well, in this case, the cut is exactly at , so if we show that this always exists for any set with a lower bound, then we have shown taht the Dedekind cut is closed on , which shows completeness.
Proof
Let . We want to find the infinum. Let’s construct a set as follows. We do this because the largest element of should be the infimum.
Case 1: say that has a maximal element .
This is only just one case. But we claim that is the infimum of . To do this, we claim that any is not a lower bound of .
Let’s assume the opposite for a second. Say that this is a lower bound. By the density of rational numbers, there exists some such that . Anything less than a lower bound is still a lower bound, so is a lower bound, which means that . However, we have previously established that is the maximal element, so this is a contradiction.
Case 2: the maximal element of is not in
This can totally happen! Infimums are not guaranteed to be in Q.
Let’s define a Dedekind cut . We want to show that is the infimum of .
We use a contradiction. Suppose that is not . Then, there exists some such that is a lower bound of of . We make our own Dedekind cut for as . By Dedekind cut definitions, we get that , which means that there exists some . But because , we get that is a lower bound of as well, which means [by an original definition], . We have two opposing statements, which is a contradiction.
Archimedean property 🚀
If , then for some positive integer , we have .
What this is saying is that no is infinitesimal with respect to another .
Proof
By contradiction. Suppose that there exists for all . Let be the set . Because it is bounded, the completeness axiom states that there exists a supremum . However, we also know that , so we have . Because is the least upper boound, we have some , which means that , and that’s a contradiction because and we asserted that was an upper bound.
Fields (additional topic)
Rational numbers (not natural numbers) and real numbers are fields. This means that they satisfy associativity, commutatitivy, and distribution.
Now, fields are mathematical objects; they are not derived, as they are, from Peano axioms. They are just a label we slap onto certain mathematical spaces and it is helpful.
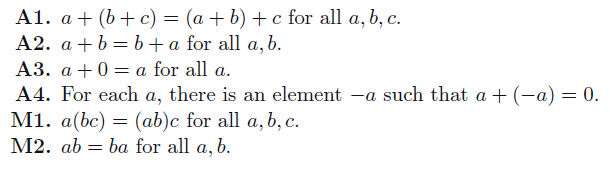
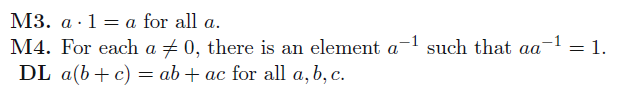
The theory of rational numbers and real numbers rests on these (often obvious) properties. There are some natural consequences to field properties
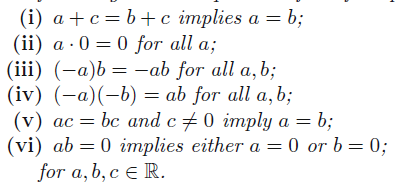
Proof sketches
- Additive inverse -c
- Let (A3). Distribute, and then use A3 again to get , and by (1), you get that .
- Use additive inverse to get , which means that .
- Use additive inverse to get , then use IV to get , and the rest is trivial
- M3 multiplicative inverse
- Start with . We know that a multiplicative inverse exists, so .
Ordered fields
What’s more, rational and real numbers are ordered fields, which means that there are a few additional properties that hold
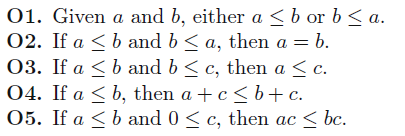
These yield certain results
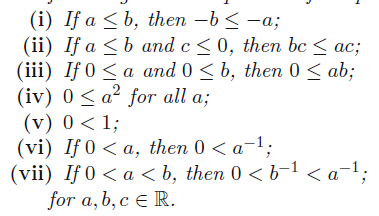
Proof sketches
- Let . Then, through O3 it becomes .
- Just negate the , apply O5, and then apply (i)
- Use O5 with , which gets you .
- If is positive, apply (iii) directly. If is negative, then we know that , yielding from (iii). From fields, we’ve established that .
- ??
- Proof by contradiction. If , then we have , but if we multiply it by which is a positive nuimber, we get that , which is invalid.
- ??
Practical Max and Min Advice
- (same as triangle equality)
-
-
Proof (contradiction)
If , then we have no problem. This satisfies the equation. But let’s say that this wasn’t the case. Then, we just need to take and compute . Because , then we have .
-
Unfortunately, you can’t say much about unless all .