PROOF TIPS

• if you have a relationship of $a_n, a_m$, try using cauchy (for sequences and series)
  • if you have relationship of $a_n, a_{n+1}$, try to expand it into something general, like $n + k$.

• split sums into finite and infinite portions

• use geometric properties.

Infinite sums

Partial sums 🐧

We denote $s_n = \sum_{k = m}^n a_k$, which is a partial sum. Here, we care less about what this $m$ is. We denote the infinite sum as $\lim s_n = S$.

Because this $s_n$ is just another sequence, we can talk about series convergence by just talking about the limit of the partial sum! This is really helpfl

If a series doesn’t converge, we say that it diverges. We can say that it diverges to $\pm \infty$ if that’s relevant. Sometimes, we write the summation in shorthand $\sum a_k$ if we know it’s infinite summation and we don’t care about the starting point.

We say that a series absolutely converges if $\sum |a_k|$ converges. We will see a theorem about this later.

Geometric and harmonic series 🧸

If we are asked to compute the formula for a certain geometric series, we can try to derive a general formula for $s_n$, and then take the limit

• Example with $\sum \frac{1}{3^i}$

  We know that $s_1 = 1/3, s_2 = 4/9, s_3 = 13 / 27$. You see that the general formula is

  $$s_n = \frac{(3^n-1)/2}{3^n} = \frac{1}{2} - \frac{1}{2*3^n}$$

  and by limit lemmas, we know that $\lim s_n = \frac{1}{2}$, which means that the infinite sum is just $\frac{1}{2}$.

We can show easily a general formula for geometric series

• Derivation

  Let’s look at $\sum 1/r^i$, where $r > 1$.

  We know that $s_n = 1/r + … + 1/r^n$, and we also know that $\frac{1}{r}s_n = \frac{1}{r^2} + … + \frac{1}{r^{n+1}}$.Therefore, if we take the difference, we get

  $$s_n(1-\frac{1}{r}) = \frac{1}{r} - \frac{1}{r^{n+1}}$$

  which means that

  $$s_n = \frac{1/r - 1/r^{n+1}}{1 - 1/r}$$

  When we take the limit, this $\frac{1}{r^{n+1}}$ term goes to 0, which yields

  $$\lim s_n = \frac{1/r}{1 - 1/r}$$

  if if you start with $i = 1$. If you start with $i = 0$, it’s just $1 / (1 - 1/r)$, and you can multiply it by an initial term to yield the formula you know and love: $a / (1 - 1/r)$.

In general, a harmonic series $\sum \frac{1}{n^p}$ converges only if and only if $p > 1$. For even $p$, you can derive closed form summations, but for odds, we don’t have a solution.

Cauchy Criterion 🐧⭐

We can just apply the cauchy criterion to the partial sums. If we have $|s_n - s_m| < \epsilon$, then our series converges.

We c an also rephrase it as

Boundedness 🚀

If $a_n \leq b_n \leq c_n$ and $\sum a_n, \sum c_n$ converge, then we know that $\sum b_n$ converges.

• Proof (by partial sums and cauchy)

  We essentially want to show that $|s^b_n - s^b_m| < \epsilon$. But we already know that $|s^a_n - s^a_m| < \epsilon$, and $|s^c_n - s^c_m| < \epsilon$. Note that $s^a_n - s^a_m = a_{m} + … + a_n$, and $s_n^c - s_m^c = c_m + … + c_n$.

  Because we have $a_n \leq b_n \leq c_n$ for all $n$, we conclude that

  $$-\epsilon < s^a_n - s^a_m \leq s^b_n - s^b_m \leq s^c_n - s^c_m < \epsilon$$

  which means that

  $$|s_n^b - s_m^b| < \epsilon$$

  as desired.

Tests

Convergence test 🚀🔨

If a series converges, then $\lim a_n = 0$. Contrapositive: if $\lim a_n > 0$, then a series diverges.

• Proof

  We know that $|s_{n+1} - s_n| = |a_{n+1}| < \epsilon$, which means that $|a_{n+1} - 0| < \epsilon$, which means that $\lim a_{n+1} = 0$.

  This does NOT go the other way. It is possible to have sequences like $1/n$ that converge but the series diverges.

Absolute convergence corollary 🚀⭐

Absolutely convergent series are convergent. The converse is not generally true.

• Proof

  We know that $-|a_n| \leq a_n \leq |a_n|$. If both the left and right sides are convergent, then $a_n$ must be convergent.

As an aside: for series, $\sum |a_n|$ converges means $\sum a_n$ converges, which means that if $\sum a_n$ diverges, then $\sum |a_n|$ must diverge or else we get a truth table problem. When in doubt, sketch out a truth table!

for sequences, $a_n$ converging means $|a_n|$ converging, but it is certainly not the case the other way around.

Comparison test 🚀🔨

Let $\sum a_n$ be a series with non-negative terms.

1. If $\sum a_n$ converges and $|b_n| \leq a_n$ for all $n$, then $\sum b_n$ converges

2. If $\sum a_n = \infty$ and $b_n \geq a_n$ for all $n$, then $\sum b_n = \infty$.

• Proof

  First point: From triangle inequality, we have

  $$|\sum b _k| \leq \sum |b_k| \leq \sum a_n \leq |\sum a_n|$$

  Since we know that $|\sum a_n| < \epsilon$, and we know the inequality above, we have that $|\sum b_k| < \epsilon$, which is what we wanted to show.

  Second point: this one is easier. Let $t_n, s_n$ be the infinite sums of $b_n, a_n$ respectively. If $b_n \geq a_n$, then $t_n \geq s_n$ for all $n$, and if we know that $\lim s_n = \infty$, it must be that $\lim t_n = \infty$.

Ratio test 🚀🔨

If $a_n$ is non-zero, we can take $r = \lim |a_{n+1} / a_n|$.

1. If $r > 1$, then the series diverges

2. if $r < 1$, then the series converges

3. if $r = 1$, we get no further information

The intuition is as follows: if $|a_{n+1}| \approx r|a_n|$, you can see this as a geometric sequence. If it’s a geometric sequence, then we know that if $r > 1$, then things diverge, and if $r < 1$, then things converge. We can’t just say this directly because it’s limit behavior.

• Proof (limit definitions, intermediate value trick, and summation splitting)

  By limit defintions, we have $|a_{n+1}| / |a_n| - r| < \epsilon$ for some $n > N_\epsilon$. Our goal is to show that $a_{n+1} / a_n$ behaves geometrically past a certain point.

  Show divergence: Now, a good strategy to approach this sort of proof is with the number line.

  

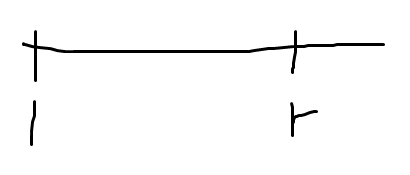
  because $r > 1$, we know that $(r+1)/2 > 1$. We also know that $(r + 1)/2 + (r - 1)/2 = r$. Thils looks like

  

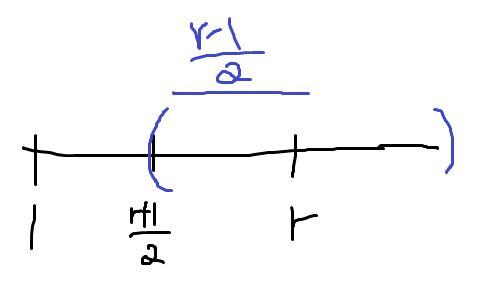
  which means that we can let $\epsilon = (r-1)/2$, and we have $|a_{n+1}|/|a_n| - r > -\epsilon > (1-r)/2$ for some $n > N_\epsilon$. Therefore, we have $|a_{n+1}|/|a_n| > (1 + r)/2 > 1$ for all $n > N_\epsilon$. All of this is to say that the sequence will become larger and larger and so it will not converge to $0$. Therefore, the series must diverge.

  We used the middlepoint argument because we wanted to show that this ratio is larger than 1 from the knowledge that it approaches $r$. The argument is quite standard, and it’s the intermediate value theorem.

  Show convergence The idea is the same. We want to show that the ratio goes below 1 for some $n > N_\epsilon$. We can do this in a similar intermediate value proof.

  Because $r < 1$, we know that $(r + 1)/2 < 1$. We also know that $(1 - r)/2 + (r + 1)/2 = 1$. We can let $\epsilon = (1 - r)/2$, which yields $|a_{n+1}| / |a_n| - r < \epsilon = (1 - r)/2$ which mean that $|a_{n+1}| / |a_n| < (r + 1)/2 < 1$. Now, we aren’t exactly done yet. To show convergence, we can use the bounding theorems. If we fix some $n > N_\epsilon$, we have $|a_{n+k} | < ((1+r)/2)^k |a_n|$. Therefore,

  $$\sum_k |a_{n+k}| < |a_n|\sum_k (\frac{1+r}{2})^k$$

  and because we established that $(1 + r)/2 < 1$, the right hand side converges. By the bounding theorem, we know that the left hand side converges. Therefore, we know that $\sum_k|a_{n+k}|$ converges. And the first half, $\sum_n^k |a_n|$ is finite. So, it must converge. If both parts converge, then the whole thing converges absolutely, which means that the series converges.

  The general skill here is after you see that a sequence increases by a constant ratio after a point, you can just rearrange it into a geometric series after that point.

Root test 🚀🔨

Let $a_n$ be a series and let $r = \lim|a_n|^{1/n}$. The series

1. Converges absolutely if $r < 1$

2. Diverges if $r > 1$

3. No further information if $r = 1$

The intuition is this: we can rewrite it as $|a_n| = r^n$, and again, this is just like a geometric sequence.

• Proof (same trick: limit definitions, pick an epsilon, use geometric series)

  Divergence Let’s use the limit definitions. For some $n > N$, we have $||a_n|^{1/n} - r| < \epsilon$. What we eventually want to show is that $|a_n| > f(r)^n$ for some mysterious function $f(r) > 1$. We use the exact same trick as the ratio test! Let’s find an $\epsilon$ such that $r - \epsilon > 1$, and we are done. Consider $\epsilon = (r - 1)/2$, and $r - \epsilon = (r + 1)/2 > 1$. Therefore, we have $|a_n| > ((r+1)/2)^n$. this doesn’t converge to 0, so the series can’t converge

  Convergence. Same trick, so let’s speed through it. We want $|a_n| < r + \epsilon$, and because $r < 1$, we can let $\epsilon = (1 -r)/2$, which means that $r + \epsilon = (1 + r)/2 < 1$. Therefore, we have $|a_n| < ((r + 1)/2)^n$. We can use the same bounded case to show that $\sum_{n = N_\epsilon}^\infty |a_n|$ converges, and the first part must be finite, so the whole series converges.

Cauchy Condensation test

A decreasing, non-negative series $\sum a_n$ converges if and only if $\sum 2^n a_{2^n}$ converges.

With this trick, you can easily prove why harmonic series converge or diverge.

• Proof

  Forward direction: this is pretty easy as $a_n$ decreases and you can expand the summation of the condensate

  Backward direction: you can show that $\sum 2^n a_{2^n} < 2 \sum a_n$ by alligning the components. The insight here is that $\sum 2^n = 2^{n+1} - 1$. The left hand side is the $\sum 2^na_{2^n}$ expanded out, and the right hand side is the counting by doubles.

Euler Number

We define the euler number as

• Proof of convergence

  Let $a_n = \sum_i^n \frac{1}{i!}$ . It is sufficient to show that $a_n$ is bounded, because we know that $a_n$ increases.

  We can show this pretty easily. We know that $i! > i^2$ for all $i > 3$ [proof by induction] so you can split up the sum into $1 + 1 + \frac{1}{2} + \frac{1}{6} + \sum_{i=4}^n \frac{1}{i!}$, which we can lower bound $1 + 1 + \frac{1}{2} + \frac{1}{6} \sum_{i=4}^n\frac{1}{i^2}$, which we know is finite due to harmonic series.

  Therefore, because it’s bounded, we conclude that this series converges. We define the value of this convergence as $e$.

Another definition is

To prove this, we first need to show Bernouli’s inequality:

• Proof

  Simple induction. Base case $n = 1$, this works by inspection.

  Inductive case: assume that it is true, and let’s start with $(1 + a)^{n+1} = (1 + a)(1 + a)^n > (1 + a)(1 + an)$, and if we expand, we get that $(1+a)^{n+1} \geq 1 + an + a + a^2n = 1 + a(n+1) + a^2n$, and because $n> 0, a^2 > 0$, then we are done.

Now, we show that the limit converges

• Proof of convergence

  To show convergence, let $x_n = (1 + \frac{1}{n})^n$ and $y_n = (1 + \frac{1}{n})^{n+1}$. Now, it is sufficien to show that $x$ increases and has a finite upper bound. Here, it is hard to show that there is a strict bound directly, but we can show that $x_n < y_n$, and then show that $y_n$ decreases. In essence, we are showing that these two sequences push towards each other, leading to a singular point of convergence.

  This requires four points

  1. $x_n$ increases

  2. $x_n \leq y_n$

  3. $y_n$ decreases

  4. $y_n - x_n → 0$

  The second point is pretty easy, because $1 + \frac{1}{n} > 1$ (just divide both sides by $x_n$ and you’ll see). The fourth point is also pretty easy because you get $y_n - x_n = \frac{1}{n}(1 + \frac{1}{n})^n$, and by limit theorems, we can just say that $\lim 1/n = 0$, so $y_n - x_n → 0$.

  So, we need to show that $x_n$ increases. One way to do this is show that $x_{n+1}/ x_n \geq 1$. If you do the algebra out,you will get the form

  $$\frac{(n+2)^{n+1}}{(n+1)^{n+1}}* \frac{n^n}{(n+1)^n}$$

  and you can massage this by adding one more to the exponent of the second fraction and dividing by $n / (n+1)$. If you do this, you wil get

  $$(\frac{n^2 + 2n}{n^2 + 2n + 1})^{n+1} * \frac{n+1}{n}$$

  and you can do the classic $+1 - 1$ trick to the numerator, which yields

  $$(1 - \frac{1}{n^2 + 2n + 1})^{n+1} * \frac{n+1}{n}$$

  and now, you can use Bernoulli’s inequality with $a = \frac{1}{n^2 + 2n + 1}$, which yields

  $$(1 + a)^{n+1} \frac{n+1}{n} \geq (1 - \frac{n+1}{n^2 + 2n + 1})\frac{n+1}{n} = 1$$

  After all of this, we conclude that $x_{n+1} / x_n \geq 1$

  We can do a similar thing with $y$, but you do it in reverse for decreasing.

Cardinality

If we have $a_n, b_n$ such that $\lim a_n = \infty, \lim b_n = \infty$, we say

• $a_n = o(b_n)$ if $\frac{a_n}{b_n} → 0$, i.e. $b_n$ becomes larger and larger than $a_n$.

• $a_n = O(b_n)$ if there exists some $c \in R$ such that $a_n \leq cb_n$ for all $n > N_0$ (just like complexity analysis)

• $a_n = \Omega(B_n)$ if there exists some $c_1, c_2$ such that $c_1 b_n \leq a_n \leq c_2 b_n$ for all $n > N_0$.

Alternating Series and Integral tests

Integral test

If a sequence decreases, then you can compute the integral. The integral converges if and only if the series converges.

• Proof (by drawing and integrals)

  

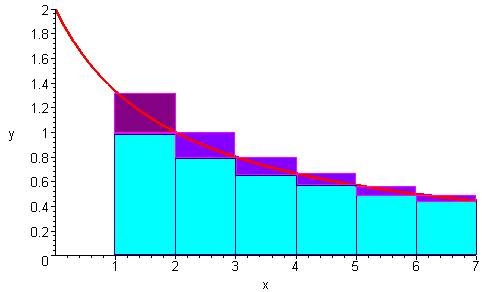
  From this, we conclude that $f(n+1) \leq \int_n^{n+1}f(n)dn \leq f(n)$, and if we take the infinite sum of both sides, we have

  $$\sum^\infty f(n+1) \leq \int_1^\infty f(n)dn \leq \sum^\infty f(n)$$

  Now, what we really want to show is the opposite squeeze, because once we show this, we can show convergence. We have one side already done: $\int_1^\infty f(n) dn \leq \sum^\infty f(n)$. Now, for the other side, we note that

  $$f(1) + \sum^\infty f(n+1) = \sum^\infty f(n) \leq f(1) + \int_1^\infty f(n)$$

  As such, we have

  $$\int_1^\infty f(n)dn \leq \sum_{n=1}^\infty f(n) \leq f(1) + \int_1^\infty f(n)$$

  and by the comparisons test, because both sides converge, it must be that the infinite summation converges.

Alternating Series test

If $a_n$ decreases and $\lim a_n = 0$, then

converges. Note that this is NOT the case for non-alternating series. A classic example is $1/n$, which satisfies decreasing and limit, but the series does not converge.

• Proof (recognizing pattern)

  We know that $s_{2n + 2} = s_{2n} - a_{2n+1} + a_{2n+2}$, and because $a_n$ decreases, we conclude that $s_{2n + 2} \leq s_{2n}$ for all $n$.

  Similarly, we know that $s_{2n + 3} = s_{2n +1} + a_{2n + 2} - a_{2n + 3}$, and with similar logic, we conclude that $s_{2n + 3} \geq s_{2n + 1}$ for all $n$. So we effectively have all even terms decreasing and all odd terms increasing.

  Furthermore, we know that $s_{2n + 2} = s_{2n + 1} + a_{2n+2}$, which means that $s_{2n + 1} < s_{2n+2}$.

  Therefore, we know that all $s_{2n + 1} < s_2$ (because it’s less than $s_{2n + 2}$, which is less than $s_2$. Because this is monotonic and bounded, we conclude that $\lim s_{2n + 1} = c$ and $c$ is finite.

  Similarly, because $s_{2n + 2} > s_{2n+ 1}$, we know that $s_{2n + 2} > s_1$, and so because it’s bounded and monotonic, we conclude that $\lim s_{2n} = c’$.

  Now what? We just need to show that these two limits are the same. This is actually trivial:

  $$|c' - c| = |\lim s_{2n + 1} - \lim s_{2n}| = \lim |s_{2n + 1} - s_{2n}| = \lim |a_{2n + 1}| = 0$$

  by limit theorems, which means that $\lim s_n = c$, and therefore it converges

Decimal Expansions

We can show that long division is just making an infinite series $d_n$ using remainders $r_n = 10 r_{n-1} - bd_n$, $0 \leq r_n < b$, and you can show through induction that

You can also show that following properties

• Every nonnegative real number has at least one decimal expansion

• Every nonnegative real number has either one decimal expansion or two expansions (ending in 0’s or 9’s)

• A number is rational if and only if it has a repeating decimal expansion