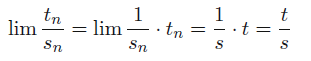PROOF TRICKS 🔨

• Proof by number line visualizations (good for intuition). Circle an epsilon radius around the point and see if you can make any deductions.

• when you are dealing with things in the form $|a - b|$, triangle inequlaity should be in your toolkit

• Never use infinite behavior for limits, i.e. you can’t say if $\lim x_n = c$, then at the limit $x_\infty = c$, as this is hard to understand. Always go back to the original definition.

• If $|a - b| < c$, we know that $a - b < c$ and $b - a < c$. You get two bounds from one.
  • conversely, to show inequality, we need to show two bounds or show that $a > b$ and $a- b < c$.

• To universalize, or to specialize?
  • If you want to show a limit exists, you need to universalize an epsilon
  • If you want to show that a certain property holds given that a limit exists, you might want to put your thumb down on an epsilon
    • Specifically, if you care about a certain property of $n$, but you can split the number line at any $N_\epsilon$.

• if you’re dealing with some bounds $M, N$, it’s often easy to let $K = \max(M, N)$ so that both are satisfied

• Redefining $\epsilon$. Sometimes, you might start with a limit definition and end with another limit definition. Therefore, it might be critical that you use some different $\epsilon$ for the first limit definition, like $|a_n - l| < \epsilon / 2$. This is legal because you can just substitute in your $\epsilon ‘ = \epsilon / 2$. However, it is helpful because maybe later you want to combine things to a singular epsilon.

• $|s_nt_n - st| = |s_n(t_n - t) + t(s_n - s)|$ “reverse distribution”

• The delta / 2 trick. This is particularly useful if you have some number $A < B$. As an example, take where $A$ is the greatest lower bound of a set $S$ and $B \in S$. You say that $B - A = \delta$, and you say that $A + \delta / 2$ is no longer a lower bound by definition of $A$, which means that there must exist another $B \in S$ between $A, A + \delta / 2$.
  • we use delta / 2 to avoid an edge case.

• split up into an infinite and finite case

Roadmap to convergence 🔨

1. If the sequence is bounded and monotonic, then it converges
   1. implicitly, we also know that it converges to the infimum or supremum

2. If the sequence is monotonic in general, then it may diverge to infinity or converge

3. If the sequence is not monotonic, then we need to use $\lim \sup, \lim \inf$ to make the judgement if the limit exists or not.
   1. However, we can also check the cauchy sequence property, because we’ve shown that a cauchy sequence is the same thing as a convergent sequence
   2. this is particularly useful if you have absolutely no idea what the limit could be, like in terms of a recursive sequence where you only get a bound, like $|a_n - a_{n+1}| < \frac{1}{2^n}$

Sequence Definitions 🐧

A sequence is just a function with a discrete domain $\{n\in \mathbb{Z} : n \geq m\}$ where $m = 0$ or $m = 1$. The function is typically denoted as $s_n : \mathbb{N} \rightarrow \mathbb{R}$, and you might denote the lower and upper bounds as $(s_n)_{n=m}^\infty$, or just $(s_n)_{n\in \mathbb{N}}$. Or, if the domain is well-established, we just use $s_n$.

The sequence yielded by $s_n$ can have repeated values, but we call the set of values as just the unique values. Sequences are denoted by $()$ and sets are denoted by $\{\}$.

The limit of a sequence is what $s_n$ approaches for large values of $n$.

We say that a sequence is bounded if $|s_n| \leq M$ for all $n$.

Absolute value definition 🐧

(this helps for certain proofs with limits)

We define the following from an absolute value

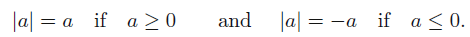
Absolute value properties 🚀

These have three properties

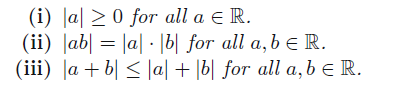
• Proof sketch

  1. If $a \geq 0$, then from our ordered field axioms, we are done. If $a < 0$, then from our field axioms, we are also done

  2. Four cases. Just enumerate them

  3. This one is actually pretty cool. We know that $-|a| \leq a \leq |a|$ and the same for $b$. Therefore, we can add them to each other, yielding

  

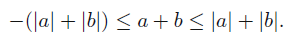
  We conclude that $a + b \leq |a| + |b|$ and that $-(a + b) \leq |a| + |b|$ , and that’s why $|a + b| \leq |a| + |b|$.

We actually call (III) the triangle inequality and it is very useful.

Whenever you get something like $|a - b| > L$, it means that $b$ is within a certain radius of $a$, so you get two inequalities from this.

Limits

Formal definition 🐧

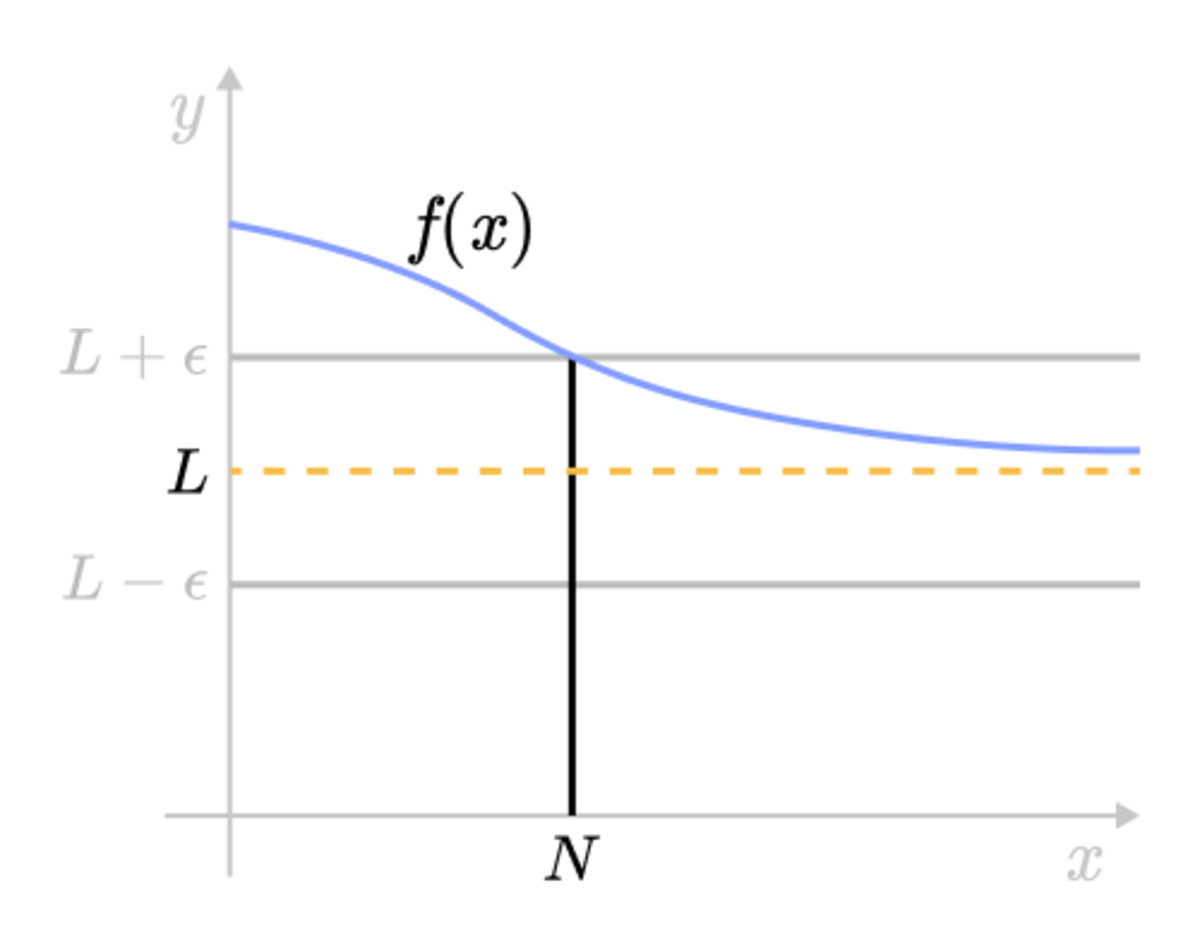
A sequence $s_n$ converges to $s$ if for every $\epsilon > 0$ there exists some $N$ such that $n > N → |s_n - s| < \epsilon$.

Conversely, we say that a sequence diverges if no such number exists (and a formal defintion, see below). It doesn’t have to diverge to infinity. it can just oscillate, like $(-1)^n$.

In english, we say that for any non-trivial radius, we can find a number large enough to satisfy this radius. This is the fundamental definition of limits and we use it to prove limit properties that we use in calculus class. We also call these delta-epsilon proofs.

Here’s a good diagram that can help

Limits to infinity 🐧

If a limit $\lim s_n = \infty$, we use the following strict definition: for all $M > 0$, there exists some $N$ such that $n > N$ implies that $s_n > M$.

In english, it means that you can always find a segment of the series larger than some number.

For negative infinity, we just say that for all $M < 0$, there exists some $N$ such that $n> N$ implies $s_n < M$.

Uniqueness of limits 🚀

if $\lim s_n = s, \lim s_n = t$, then $s = t$

• Proof (squeeze)

  If we assume that such $s, t$ exist, then we have some $|s_n - s| < \epsilon/ 2$, and we also have $|s_n - t| < \epsilon / 2$. These $n$’s might have different $N_1, N_2$ though.

  By the triangle inequality, we have

  $$|s - t| = |(s - s_n) + (s_n - t)| \leq |s - s_n| + |s_n -t| < \epsilon / 2 + \epsilon / 2 = \epsilon$$

  Therefore, $|s - t| < \epsilon$ for all $\epsilon > 0$, so it must be that $|s - t| = 0 → s = t$.

  Note that we used triangle inequality because we wanted to squeeze things.

• Alternative proof (contradiction by choosing epsilon)

  We try a contradiction. We set a value $\delta = |t - s|$. By the limit defintion, if we let $\epsilon = \delta / 4$, we have $|s_n - s| < \delta / 4$ and $|s_n - t| < \delta / 4$. We also know that

  $$|s_n - s + (-s_n + t)| \leq |s_n - s| + |s_n - t| < \delta / 2$$

  However, we’ve established that the left hand side is $|t - s| = \delta$, and it’s not true that $\delta < \delta / 2$, so we get a contradiction.

Tricks about proofs 🔨

When we prove a limit goes to $s$, we let $\epsilon > 0$ and we want to end up at some definition of $N$ in terms of $\epsilon$ such that $n > N → |s_n - s| < \epsilon$.

To do this, we often work backwards. We start with $|s_n - s| < \epsilon$. Because $s_n$ is a function, we can often move things around in the inequality such that we have an inequality $n > f(\epsilon)$, and then we let $N = f(\epsilon)$, and then you show the forward direction.

• Example proof

  Show that $\lim 1/n^2 = 0$. Proof: let $N = \frac{1}{\sqrt{\epsilon}}$. If $n > N$, then $n > \frac{1}{\sqrt{\epsilon}}$, which means that $n^2 > \frac{1}{\epsilon}$, implying that $\epsilon > \frac{1}{n^2} = s_n = |s_n - 0|$ which is the claim we wanted to show. See how we went forward in the definition, but to get the original $N$, we went backwards.

For harder functions, you have a few tools in the toolkit

• You don’t have to show the smallest possible $N$. So, you can upper bound $s_n - s$ to a simpler function $s^*_n$, and show that $s^*_n < \epsilon$ by finding an $N$ (pro-tip: you are often given two bounds: one where the upper bound is satisfied, and one where $s^*_n < \epsilon$ is satisfied. The $N$ must be the maximum of those values). [KEY FACT: you’re bounding $s_n - s$, NOT $s_n$.]
  • for divergences, consider lower bounds, which are the exact opposite

• If a limit exists for $\epsilon$, it also exists for $K\epsilon, K \geq 0$.

Disproving limits (proving divergence) 🔨

You can either

• Assume that it converges and derive a contradiction

• Show that for all $N$ and $L$, there exists some $\epsilon > 0$ such that $|a_n - L| > \epsilon$ for some $n, N > n$.

• show that two subsequences yield two different limits (more on this later)

Limit Theorems

List of proven theorems 🚀

1. If $a_n \leq b_n$ for all $n > K$, then $\lim a_n \leq \lim b_n$

• Proof (start with contradiction, and use epsilon to show contradiction)

  Let $\lim a_n = a, \lim b_n = b$. Suppose that $b > a$. Then, $b - a > 0$, and we can set $\delta = b - a$. Now, we know that $|a_n - a| < \delta / 4$ for some $n > N’$, and $|b_n - b| < \delta / 4$ for some $n > N’’$. Let $N = \max(N’, N’’)$. From triangle inequality, we get

  $$|a_n - a + (b - b_n)| = |b - a| \leq |a_n - a| + |b_n - b| < \delta / 2$$

  But we just defined $\delta = b - a = |b - a$, so we get a clear contradiction: $\delta < \delta / 2$. Where does the contradiction come from? Assuming that $b - a > 0$!

2. Convergent sequences are bounded

• Proof (Pick epsilon and show boundedness)

  Let $s = \lim s_n$. We are dealing with $|s_n - s| < \epsilon$, and a useful trick is to put a hand on $\epsilon$, because that’s not the number we are trying to show. We are trying to show across $n$.

  Let $\epsilon = 1$, so we have $|s_n - s| < 1$ for some $n> N_1$. This means that $s_n < s + 1$ and $s_n > s - 1$. Automatically, we get upper and lower bounds for $n > N_1$. Now, we do have all $n \leq N_1$, but this is a finite discrete set, so it also has upper and lower bounds. Select the upper bound as either $s + 1$ or $\max(s_n, n < N_1)$, depending on which one is larger. Similarly for the lower bound.

3. $\lim(ks_n ) = k\lim s_n$.

• Proof (direct proof through limit definitions)

  let $s$ be the limit. In this case, we have $|s_n - s| < \frac{\epsilon}{|k|}$, as we can just make a new $\epsilon’ = \epsilon / |k|$. So, we can just mlutiply everything through to get $|ks_n - ks| < \epsilon$, proving that $ks$ is the limit of $ks_n$.

4. $\lim(s_n) + \lim(t_n) = \lim(s_n + t_n)$

• Proof (direct proof through limit definitions)

  Similar technique. We know that $|s_n - s| < \epsilon / 2$, and $|t_n - t| < \epsilon / 2$ for all $n > \max(N_s, N_t)$ (where N_s, N_t were the original bounds).

  We add them together and use the triangle inequality

  $$|s_n + t _n - (s + t)| \leq |s_n -s| + |t_n - t| < \epsilon$$

  and so we showed that $s+ t$ is the limit.

5. $\lim(s_nt_n) = (\lim s_n)(\lim t_n)$
   1. Corollary $\lim((s_n)^k) = (\lim(s_n))^k$.

• Proof (use definition of limits and boundedness)

  We start by using a trick:

  $$|s_nt_n - st| = |s_n(t_n - t) + t(s_n - s)|$$

  which by the triangle inequality yields

  $$|s_nt_n - st| \leq |s_n||t_n - t| + |t||s_n - s|$$

  We get a hint of how it will play out. We know that $|s_n| < M_s$ for some $M$, because it’s bounded. We also know that $|t_n - t| < \epsilon / 2M_s$ (because you can just redefine what $\epsilon$ is. Similarly, we know that $|t| < M_t$ and we can set $|s_n - s| < \epsilon/2M_t$. From this, we know that

  $$|s_n||t_n -t| < \epsilon/2$$

  and

  $$|t||s_n-s| < \epsilon / 2$$

  which means that $|s_nt_n - st| < \epsilon$, as desired.

6. $\lim(\frac{1}{s_n}) = \frac{1}{s}$ if $s_n \neq 0$

• Proof (use boundedness)

  We establish that

  $$|s - s_n| < \epsilon m|s|$$

  as $m|s|$ are two constants that can be part of the epsilon. Now, we know that

  $$|\frac{1}{s_n} - \frac{1}{s} | = \frac{|s - s_n|}{|s_ns|}$$

  And we also assume that $s_n$ is bounded by $m$ (as it converges). So we know that

  $$\frac{|s - s_n|}{s_ns} < \frac{|s - s_n|}{m|s|}$$

  and using the original definition, we get

  $$\frac{|s - s_n|}{ms} < \frac{\epsilon m|s|}{m|s|} = \epsilon$$

  and we are done.

7. $\lim(\frac{t_n}{s_n}) = \frac{t}{s}$

• Proof

  From previous theorems, we get that

  

8. If $a_n \leq b_n \leq c_n$ and $\lim a_n = \lim c_n = r$, then $\lim b_n = r$

• Proof

  If we assume that $\lim b_n$ exists, then $b_n \leq c_n$ implies that $\lim b_n \leq \lim c_n$ (see theorem (1)). Repeat this for the other side, and you get $\lim a_n \leq \lim b_n \leq \lim c_n$, and so $r \leq \lim b_n \leq r$, and this forces us to conclude that $\lim b_n = r$.

Proven limit corollaries 🚀

• $\lim \frac{1}{n^p} = 0$

• $\lim a^n = 0$ if $|a| < 1$

• $\lim n^{1/n} = 1$

• $\lim a^{1/n} = 1$

Infinite limit theorems 🚀

1. If $\lim s_n = \infty$ and $\lim t_n > 0$, then $\lim s_n t_n = \infty$.

• Proof

  Because $s_n$ is unbounded, we know that for all $M$, there exists some $N_1$ such that $n > N_1$ implies that $s_t > M$.

  If we select a real number $0 < m < \lim t_n$, then we know that $t_n > m$ for some $n > N_2$.

  Therefore, for all $n > \max(N_1, N_2)$, we have $s_nt_n > Mm > \frac{M}{m}m = M$, as desired.

2. $\lim s_n = \infty$ if and only if $\lim(\frac{1}{s_n}) = 0$. (assuming that $s_n > 0$.). The opposite is NOT true: if you know that $\lim s_n = 0$, then you don’t know that $\lim 1/s_n$ is. Take $s_n = (-1)^n/n$, for example.

• Proof

  We show both directions.

  Forward direction: let $\epsilon > 0$ and define $M = \frac{1}{\epsilon}$. This is legal, because the range of $M$ is still $M > 0$. Therefore, there exists some $N$ such that $s_n > M = \frac{1}{n}$ for all $n > N$. Therefore, we have $\epsilon > \frac{1}{s_n}$. Because $s_n > 0$, we have

  $$|\frac{1}{s_n} - 0| < \epsilon$$

  which proves the forward direction.

  Backward direction. Use a slightly inverted way of thinking. Let $M > 0$ and let $\epsilon = \frac{1}{M}$. By definition, there exists some $N$ such that $|\frac{1}{s_n} - 0| < \epsilon = \frac{1}{M}$.

  Because $s_n > 0$, we have $\frac{1}{s_n} < \frac{1}{M}$, which means that $M < s_n$ for all $n > N$, and so we are done.

Computing vs proving limits 🔨

If you want to show that $\lim s_n = s$, then you whip out your formal definitions and you might do some lower bounding, upper bounding, etc.

If you want to compute a limit, you need to work from the limit lemmas

Tricks for computing limits

• Fractions are your friend. If you don’t have a fraction, make one! A common trick is to

Monotone Sequences

A sequence monotonically increases if $a_{n+1} \geq a_n$ for all $n \in \mathbb{N}$. We are talking about monotone sequences because it can help us show convergence even if we don’t know the exact limit.

Bounded Monotone Theorem ⭐

Theorem (1): if a sequence is monotonically increasing and has an upper bound, then it converges.

• Proof

  Let the limit of $s_n$ be $s = \sup(S)$, where $S = \{s_n, n \in \mathbb{N}\}$. We want to show that $|s_n - s| < \epsilon$.

  Well, we invoke the supremum definitions and say that $s - \epsilon$ can’t be an upper bound, so there must exist some $s_{N_\epsilon}$ such that $s_{N_\epsilon} > s - \epsilon$. Now, we also know that $s_n > S_{N_\epsilon}$ for all $n > N_\epsilon$, so we have $s_n > s - \epsilon$. Therefore, we have $s - s_n < \epsilon$, and because $s > s_n$ (supremum definition), we also say that $|s - s_n| < \epsilon$, which is the limit definition.

Corollary: the limit of a bounded monotoically inceasing sequence is $\sup(S)$, where $S = \{s_n, n \in \mathbb{N}\}$. We just assumed that this is true and proved it in the proof above which also proved theorem 1.

Theorem (2): if a sequence is monotonically decreasing and has a lower bound, then it converges. The proof is exactly the same approach as above, the the correlary is that the limit of a bounded monontonically decreasing sequence is $\inf(S)$.

Using this theorem 🔨

Sometimes, you can have sequences that are defined recursively and it’s very nasty to compute the actual limit. However, if you can show that the sequence is monotonicaly increasing and has an upper bound (or vice versa), you can show that it indeed has a limit.

More specifically, you need to show that $a < s_{n+1} < s_n$, which means that it’s a monotone sequence. You might proceed inductively and say that we assume that this is true and then show that $s_{n+2} < s_{n+1}$. If this is legal, you will get back some fact about $s_{n+1}$ which is assumed in the inductive hypothesis. Often, you need to provide a lower bound if you want to show that the sequence is decreasing (not just to use the theorem but also to show that it is monotonic). Conversely, you often need to provide an upper bound if you want to show that the sequence is increasing. These are just vague tips which can come in use.

Application: Cauchy Cantor / Nested Interval Theorem 🧸

This theorem states that there exists at least one $x$ such that

Where $[a_{n+1}, b_{n+1}] \subseteq [a_n, b_n]$. Graphically, it means that if we apply tighter and tighter bounds, we will eventually converge to a non-empty interval.

• Proof (uses monotonic sequences and inf/sup relationship)

  By bound definitions, we know that $a_n \leq b_n$ for every $n$.

  To prove this, we just want to show that $\cap[a_n, b_n] = [\lim a_n, \lim b_n]$, set-wise. This is because we know that $[\lim a_n, \lim b_n]$ is non-empty, and therefore the original thing is non-empty.

  We need to show two directions. Direction 1: $x \in \cap [a_n, b_n] → x \in [\lim a_n, \lim b_n]$.

  For this direction, we use a proof by contradiction because there are ton of restrictions to do the forward directions. So let’s suppose that $x \notin [\lim a_n, \lim b_n]$.

  Case 1: $x < \lim a_n$. Intuitively, this is a contradiction because you can pick some $a_m$ such that $x < a_m$, which means that it wouldn’t satisfy the bounds $[a_m, b_m]$. But let’s rigorize this. Because we’re using limits and we want to show something about the limit property, we try to pick an epsilon. Let $\epsilon = |\lim a_n - x|$. Therefore, there must exist some $N$ such that for all $n > N$, we have $|a_n - \lim a_n| < \epsilon / 2$. And graphically, this means that there exists this $a_m > x$, which yields a contradiction.

  Case 2 is done in a similar way

  Direction 2: $x \in [\lim a_n, \lim b_n] → x \in \cap [a_n, b_n]$

  This direction is actually pretty simple. We know that $x \geq \lim a_n$ which means that $x > a_n$ for all $n$ as $a_n$ is monotone. Similarly, we know that $x < \lim b_n$ which means that $x < b_n$ because it’s monotone.

Subsequences

Definition 🐧

A subsequence is defined as $t_k$, where $k$ indexes a sequence of monotonic numbers $n_1, …, n_k, n_{k+1}, …$ which are used to index the original sequence $s_n$. In other words,

which we can understand as selecting a bunch of $s_n$’s taken in order. All subsequences are infinite.

We can also understand it as a function composition. We can see the sequence $s_n = s(n)$, and our selection as $\sigma(k)$. The subsequence is $t_k = t(k) = s(\sigma(k))$.

Same-subsequence theorem 🚀

If a sequence converges, then every subsequence converges to the same limit

• Proof

  Let $s_{n_k}$ be a subsequence of $s_n$. We know that $n_k \geq k$ for all $k$ (think about it…or show it inductively). Let $s = \lim s_n$ . Therefore, $|s_n - s| < \epsilon$. If $k > N$, then $n_k > N$, so $|s_{n_k} - s| < \epsilon$. Therefore, $\lim_k s_{n_k} = s$.

As an aside, if a sequence diverges, it is not the case that every subsequence diverges. Consider the example $a_n = (-1)^n$. You can select all odd $n$ and this converges.

As another aside, if a sequence has two subsequences with different limits, then the sequence diverges.

Boizano-Weirstrass Theorem ⭐🚀

Every bounded sequence has a convergent subsequence.

To prove this, it is sufficient to show that you can make a monotonic subsequence from any sequence, and then by the monotonic sequence theorem, we conclude that it converges.

• Proof (infimum definitions, delta / 2 contradiction trick)

  Let $s_n$ be the set $\{a_k, k \geq n\}$. Because $a_k$ is bounded, we know that $\inf s_n$ is finite. We define $I_n = \inf s_n$

  Graphically, you can imagine this $n$ being a vertical line in the sequence plot, $s_n$ being everything to the right of it, and $I_n$ being the greatest lower bound of whatever is to the right of $n$.

  Case 1: $\inf s_n$ is in the set $s_n$ for all $n$. Say you have a subsequence $n_1, …, n_{k-1}$ so far. This means that $s_n$ has a minimal element, $a_m$. If this is the case, then assign $m = n_k$, and make a new set $s_{m + 1}$ (i.e. chop off everything up to and including this $m$ term in the original sequence). Now, we know that that $\inf s_{m + 1} \geq \inf s_{n_{k - 1}}$ because it’s a subset (we removed one element). Therefore, when we pick the next element according to this rule, it will be at least as large as $a_{n_k}$, meaning that it is monotonic.

  Case 2: There exists some $N$ such that $\inf s_N$ is not in $s_N$. Now, consider the last element $a_{n_{k-1}}$. The distance $a_{n_{k-1}} - \inf s_N = \delta$ which is non-zero. Now, consider $\inf s_N + \delta/ 2$, which can’t be a lower bound. Therefore, there must be some $a_{n_k} > \inf s_N$ and $a_{n_k} < \inf s_N + \delta / 2$, and by construction, $a_{n_k} < a_{n_{k-1}}$. Note that this $n_k > s_N$ by construction. We can keep doing this for any $N$, and so we construct a monotonically decreasing subsequence.

Subsequence-convergence theorem (extra) 🚀

Theorem: if $s_n$ is a sequence, then

1. There will be a subsequence of $s_n$ that converges to $t$ if and only if $\{ n \in \mathbb{N} : |s_n - t| < \epsilon\}$ is infinite for all $\epsilon > 0$

2. If $s_n$ is unbounded above, it has a subsequence with limit $\infty$

3. If $s_n$ is unbounded below, it has subsequence with limit $-\infty$.

Subsequential limit (extra) 🐧

We define the subsequential limit as the limit of any subsequence of $s_n$. Now, if $s_n$ converges, then we know that there is only one such limit. But if $s_n$ doesn’t have a limit originally, then we are in interesting territory. We can define $\{s\}$ as the set of subsequential limits of $s_n$.

Subsequential limits and lim sup, lim inf (extra) 🚀

For any sequence, there exists a monotonic subsequence whose limit is $\lim \sup s_n$ and a monotonic subsequence whose limit is $\lim \inf s_n$.

We can unify the idea of $\{s\}$ in this theorem:

if $S = \{s\}$, i.e. the set of subsequential limits of $s_n$, then

1. $S$ is non-empty

2. $\sup(S) = \lim \sup s_n$ and $\inf S = \lim \inf s_n$

3. $\lim s_n$ exists if and only if $S$ has only one element, $\lim s_n$.

• Proof

  1 is the immediate consequence of the previous theorem, because there must exist at $\lim \sup s_n$ and $\lim \inf s_n$, which is at least one number or symbol

  2 we can use the definitions. Consider any limit $t$ of subsequence $s_{n_k}$. Then, we have $t = \lim \inf s_{n_k} = \lim \sup s_{n_k}$. Because we know that $n_k \geq k$, we have that $\{s_{n_k}: k > N\} \subseteq \{s_n : n > N\}$. Therefore, we have

  $$\lim \inf s_n \leq \lim \inf s_{n_k} = t = \lim \sup s_{n_k} \leq \lim \sup s_n$$

  and this is true for all elements in $S$, so $\lim \inf s_n \leq \inf S \leq \sup S < \lim \sup s_n$. From the previous theorem, we know that $\lim \inf s_n, \lim \sup s_n \in S$, and so we know our greatest lower bound and our least upper bound

  3 is a reformulation of the lim-sup convergence theorem

Lim Sup and Lim Inf

Defining $\lim \sup$ 🐧

We define the following

Again, unlike our discussion above, we don’t restrict $s_n$ to be bounded, so this can be infinite. In our previous discussion, we had $\sup \{s_n: n \in \mathbb{N}\}$. Consider a function that decays over time to zero. The supreum will be much larger than $\lim \sup s_n$, which goes down to zero.

Properties of lim-sup 🚀

The $\lim \sup s_n$ is basically taking the supremum of a bound, and the limit is drawing the bound tighter and tighter. Therefore, it must be the case that

for any $N$. Simialrly,

this is true for any inf and sup: if the modifying function is monotonic, then $\inf f(s_n) = f(\inf(s_n))$. This is because it just moves the elements of the set without mixing up their order. Same for sup.

Lim-sup Theorem ⭐🚀

The bounded sequence $\{a_n\}$ converges if and only if $\lim \inf a_n = \lim \sup a_n$.

• Proof (forward: limit definition moving to infimum and supremum definition. Backward direction: sandwich theorem)

  (we need bounded, because not all sequences have $\inf a_n, \sup a_n$.

  Forward direction: if $a_n$ converges, then let $l = \lim a_n$. Now, we know that $|a_n - l| < \epsilon$ for all $n > N_\epsilon$. Graphically, this looks like a region $(l - \epsilon, l + \epsilon)$ where all $a_n, n > N_\epsilon$ lie.

  Let $i_n = \inf \{a_k, k > n\}$. Therefore, $l - \epsilon \leq i_{N_\epsilon}$. If we define $s_n = \sup\{a_k, k > n\}$, then $l + e \geq s_{N_\epsilon}$. We know by default that $i_{N_\epsilon} \leq S_{N_\epsilon}$, which means that

  $$l - \epsilon \leq i_{N_\epsilon}\leq s_{N_\epsilon} < l + \epsilon$$

  Now, this is actually true for all $n > N_\epsilon$ because of the construction of $i$ and $s$, as the larger the $n$, the smaller the subset. Infimums of subsets are always larger than the original set, and supremums of supsets are always smaller than the original set.

  So, if we have $l - \epsilon \leq i_n \leq s_n \leq l + \epsilon$, for all $n > N_\epsilon$, and we recognize that this means that $|i_n - l| < \epsilon, |s_n - l| < \epsilon$, which satisfy the limit definitions as desired.

  Overall:

  1. Expand limit definition

  2. Recognize infimum and supremum

  3. Recognize that we can reshape the inequality into limits

  Backward Direction: if $\lim \inf a_n = \lim \sup a_n$, then $a_n$ converges.

  Well, this one is trivial. We know that $\inf \{a_k, k \geq n\} \leq a_n \leq \sup\{a_k, k \geq n\}$ by definition, for all $n$. By the sandwich theroem, if the limits are the same, then we have $\lim \inf a_n= \lim a_n = \lim \sup a_n$

Cauchy Sequences

The definition 🐧

A sequence is a Cauchy sequence if for every $\epsilon > 0$, there exists some $N$ such that $m, n > N$ implies that $|s_n - s_m| < \epsilon$.

Graphically, it looks like a certain radius in which all pairwise elements are within some $\epsilon$ distance of each other.

Cauchy equivalence to convergence ⭐🚀

Theorem: a sequence is a convergent sequence if and only if it’s a cauchy sequence

• Proof (forward: triangle inequality. Backward: picking an epsilon, proof by contradiciton starting with cauchy and incorrect assumption about limits yielding contradiction)

  Forward direction: if $a_n$ is convergent, then $|a_n - l| < \epsilon/2, |a_m - l| < \epsilon/2$ for all $m, n > N_\epsilon$. Using the triangle inequality, we have $|a_n - a_m| \leq |a_n - l| + |l - a_m| < \epsilon$, which is the definition of a cauchy sequence.

  Backward direction: We want to show that a cauchy sequence is bounded and $\lim \inf = \lim \sup$, which allows us to show that the sequence converges.

  Let’s start by showing that the cauchy sequence is bounded. We start with $|a_n - a_m| < \epsilon$ for some $n, m > N_\epsilon$. Now, we want to show that the whole sequence is bounded, and we see a reasonable split between $0 → N_\epsilon$ and $N_\epsilon → \infty$. The location of the split is arbitrary. So, let $\epsilon = 1$.

  Therefore, $|a_n - a_m| < 1$ for all $n, m > N_1$. We can put our thumb down on some $m = N_1 + 1$. Therefore, we have $a_n < 1 + a_{N_1 + 1}$ for all $n > N_1$. This last step is another good trick to have, because we are eventually pushing towards the bounding case. Here, we have just accomplished that. We have shown that for all $N_1 → \infty$, all $a_n$ are below a certain fininte bound. Now, we have left the $0 → N_1$, but this is trivial because it’s a finite set. A finite set is always bounded. If the infinite $N_1 → \infty$ is bounded, and the $0 → N_1$ is bounded, then we conclude that the whole set is bounded.

  Next, we want to show that $\lim \inf = \lim \sup$.

  To do this, let $i_n = \inf\{a_k, k > n\}$ and $s_n = \sup\{a_k, k > n\}$. It is sufficient to show that $|s_n - i_n| < \epsilon$ for some $n > N_\epsilon$. You can derive this through the triangle inequality.

  Because things look a bit daunting, let’s start with a proof by contradiction. Let’s start with the cauchy assumption that $|a_{m'} - a_m| < \epsilon / 2$ for some $m, m’ > n$.

  Now, let’s say that $s_n - i_n = \delta > \epsilon$. Now, let’s pick a perturbation $\epsilon / 4$. We know that $i_n + \epsilon / 4$ isn’t a lower bound, so there exists some $a_{k_1} < i_n + \epsilon / 4$ and similarly, we know that $s_n - \epsilon / 4$ isn’t an upper bound, so there exists some $a_{k_2} > s_n - \epsilon / 4$. Note that we implicitly have $k_1, k_2 > n$.

  Now, we know that $a_{k_2} > a_{k_1}$ because $i_n > s_n$, so we get that $a_{k_2} - a_{k_1} > s_n - i_n - \epsilon / 2$. From the assumption $s_n - i_n < \epsilon$, we get that $a_{k_2} - a_{k_1} > \epsilon - \epsilon / 2 = \epsilon / 2$. This is a contradiction to the original setup by the cauchy sequence, so the whole thing is a contradiction. We are done.