The fundamentals

Start a proof by getting a general intuition for why it’s true. then, abstract it away and talk about informal terms. Lastly, put down the formal proof

Contradiction is your friend!

General form: show B from A. Immediately, you should write out the definitions of A, and the formal definitions of B. Try to see if you can massage the definitions of A to B.

• If A is a universal qualifier, see if you can select a specific case that yields B.

• If both A and B yield restrictions on sets, try to show that all elements in A belong to B.

• always try contradiction if there are too many moving parts

General form: show that there exists some X and satisfies A and B. This is an existential proof, so the best bet is to construct something iteratively such that we satisfy both A and B. Alternatively, we can show that all A belong to B, or vice versa (although this is not generally true) .

General form: show that $f(x) = f(y)$, where f is some function, x, y are inputs, where the property of y is known. Mainly, you should write out the definition of what $f(y)$ means. This $k = f(y)$ satisfies all these properties. Now, you show that this $k$ satisfies the properties of $f(x)$ as well.

General form: show that f(x) = f(y) but neither properties of x, y are known. In this case, you will need to massage $x, y$ back to something and use original truths.

General form: show that x is unique. Start by assuming that there are two x, y that satisfy a property. Then, show that $x = y$.

Using universals and the “algorithm” view

If you want to show a universal statement for some $x$, you essentially want to develop an algorithm that shows that something is true for one arbitrary $x$.

If you want to use a universal statement for some $x$, you can assume that one such function exists.

So, to show a universal statement from another one, you can say that you pick some $x’$. You might know that a universal works for $x$. Just massage this $x’$ into the input $x$ such that your final result shows that this $x’$ works for the universal.

Here’s a concrete example. Say that you wanted to show that all multiples of $6$ are even. You can express this as $6n'$. We know, as a universal, that all $2n$ are even. In this case, we can let $n = 3n’$. This is the mapping from the desired, arbitrary input to a the input that works for our assumed universal. This yields $2(3n’)$, and we can apply the universal to show that $6n’$ is even.

This is also why you can start with some $|a_n - l| < \epsilon’$ and use some $|a_n - b| < \epsilon$, and then at the end, you might show that you can write $\epsilon$ as a function of $\epsilon’$. We might have a shorthand where we start with $\epsilon’$ directly and plug in the function of $\epsilon’$ in the original definition of $\epsilon$.

When can you turn $<$ into $\leq$?

Generally, if you have some $f(x) < k$, as $x → \infty$, we can say $f(x) \leq k$. It might not be that $\lim f(x) = k$, but it is still correct to switch the bounds to an inclusive.

Bounding

• For fractions, if you want to make some $\frac{a}{b} < \frac{x}{y}$, you need to show that $a < x$ and $b > y$. (useful for complicated limits)

• Triangle inequality is your friend $|a + b| \leq |a| + |b|$. Often, you might have $|a + b|$ is a known property and you can somehow massage $a + b$ into the original $a, b$ to make a statement. Example: $a + b = 2$, which might let $a = (1 - x)$ and $b = -x + 1$.

Contradiction

If you want to show (or dissapprove) that something can be written in a form

• Assume that you can, and then derive a solution (or contradiction).

Generally, the logic flow of a contradiction starts with two coflicting definitions. You work with one definition and massage it until you see that it clearly violates the other definition. The key here is that you only go with one definition.

Tools

• we say “without loss of generality” if the proof works the same way for multiple cases.

A great table

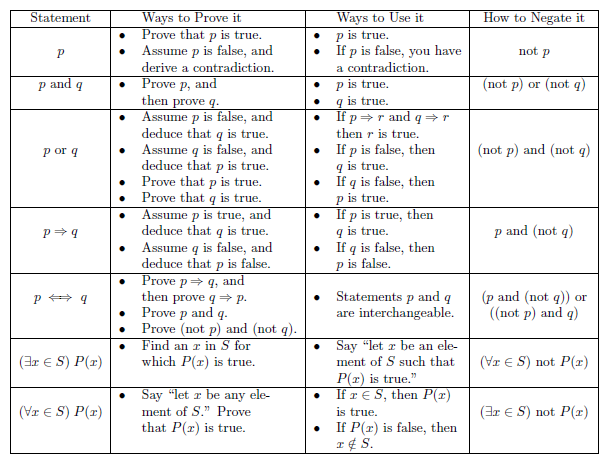
Set Facts