Notation stuff

When dealing with random variables, we typically need to say something like $p(X = x)$, but we just use a shorthand at times $p(X)$. It’s the same thing.

We use the term $Val(X)$ to get the values that the RV can take on.

More sophisticated notation

Sometime we use the $Pr\{\}$ notation if using another $P$ is confusing. This is common for CDF, or if the likelihood is a random varaible

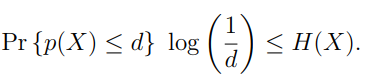
• we use CAPITAL to represent the random variable itself. So $p(X)$ means a random variable $X$ such that we run it through the probability function $p$ after sampling
  • general rule of thumb: if it’s outside of a summation, and you just want to refer to “something”, capital is the way to go.

• we use lowercase to represent a sample or an instance. So $p(x)$ is a number (shows up in summations, etc).

Distributions vs. probabilities 🐧

A distribution has no "p" attached to it. For example, $y | x \sim \mathcal{N}(x, 1)$. In this case, $y | x$ is a distribution. However, $p(y | x)$ is a probability. You can find the probability by plugging in $y$ into the CDF formula defined by $y | x$.

Prior and Posterior

The prior is what you believe before some observation. For example, $p(c = i)$. The posterior is what you believe after some observation, like $p(c = i | b)$

Densities

Here’s also a point of confusion that sounds stupid but it happens all the time. The $p$ is not a specific function. So $p(x | y)$ isn’t the same as $p(a | b)$, etc. This is true even when the $p$ is specialized for some application. Probability is not a function.

The density $p(s)$ means the likelihood of $s$, which ALSO means that if you were to select $s$ at random, the likelihood of $s$ being this current $s$ has likelihood $p(s)$.

Remember that $p(s)$ is a value, as $s$ is scalar. Therefore, $p(s | v)$ is well-defined, but NOT $p(s | V)$. The conditioning must always be deterministic. On the other hand, $p(S | v)$ is totally fine; it’s just another random variable.