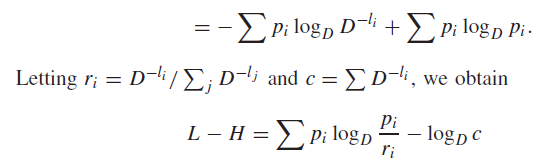Proof tips

• usually you can expand things twice, which gives you an automatic relationship (true for anything with the chain rule)

• use indicator variables as bernoulli RV’s

• upper bound probability of event $X$. If you think of $X$, does it entail event $Y$? And does this event $Y$ have an easily expressible form? If $X$ implies $Y$, then $p(X) \leq p(Y)$.

• always start from basic definitions; it helps a ton

• add and marginalize is a really big one too

• To show something about $Pr(x \in X)$, you can use this: $\sum_{x \in Y} p(x)$. Simple trick but the latter gets you to something that you might be able to calculate

• Simple tricks work best for minimally constrained problems

• Pr(X > C) express as integral, same with expectation

• Remember the mean of $n$ RV’s is just the overall mean of one RV, and the variance is the original variance divided by $n$. (sample means)

• sum of gaussians is also a gaussian

Distribution tricks

• marginalize → summation → potentially expectation

• Expand: $p(x) = p(x, y)/p(y|x)$. See if this gets you anywhere

• Marginalize: $p(x) = \sum_y p(x,y)$.

Flipping summations and expectations

This is a very critical trick in many proofs

Advanced properties of RV’s

Information lines vs dependency lines

In things like Markov chains, we draw things like $X → Y$. In communication, we might draw something like $X -[P]- Y$. What is the difference? Is there a difference?

• The $-[P]-$ indicates that there is something that messes the signal up between $X$ and $Y$. Depending on how bad it is, $I(X ; Y)$ could range from 0 to some positive number.

• The $→$ is a more vague version of this $-[P]-$ notation. We just know that there is a dependency, a distribution $p(y|x)$. This could be the same as $p(y)$, although it is generally good practice to remove the arrow if that’s the case. So there’s a subtle difference. If $X →Y$, then we know that $I(X ; Y) > 0$.

Convexity in a distribution

This is definition a mind trip, but certain things can have convexity or concavity WRT distributions. Don’t get too confused. A distribution is just a vector with L1 length 1. You can interpolate between two vectors, whose intermediate vectors are still L1 length 1. This interpolation is the secant line drawn between two distributions.

Linear function of a distribution

When we have something like $\sum_x p(x) g_x$, we say that this is a linear function of $p(x)$. Again, back to our view that a distribution is a vector. This is the same as doing a Hadamard product on the vector, which is linear.

Making distributions from nothing at all

When you’re faced with something that feels very close to a distribution, feel free to multiply by the sum and divide by the sum. Division by the sum makes the thing into a distribution

• Example

  

Some tips for spotting wannabe distributions

1. summations with indices (just divide by the summation to get a distribution). Often, you can make the summation into an expectation of something WRT a distribution .

2. things with logs and inequalities (because with a distribution, you can use Jensen’s inequality)

Why do this? Well, things like Jensen’s inequalty and expectations don’t work without a distribution, so it’s beneficial to make one.