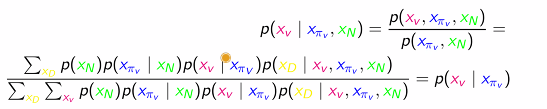Marginalization

You can expand a distribution by marginalizing:

Sum is always 1 🔨

Remember that $\int p(x) dx = 1$. Taking the derivative of $\int p(x)dx$ WRT any variable (say, an internal parameter), is always $0$.

The art of marginalization 🔨

When you need to find something like $p(a | b, c)$, your first thought should go to Bayes rule, becuase it allows you to express it as

And the unconditional probabilities can be expressed as marginalization of the joint probability, like

And the cool part is that you typically factorize the joint probability using a Bayesian network definition, and this will allow some nice simplification. Things typically collapse

• Example

  

Marginalize, unmarginalize 🔨

You can move things around by marginalizing. For example

And now that you have expanded it, you might have more options.

You can marginalize distributions, but you CAN’T marginalize something like $H(X, Y)$. This is because we already take the joint expectation and the entropy operator is not linear.

• Instead of marginalizing, consider chain rule

Marginal vs Conditional

Marginal is squashing, while conditional is slicing.

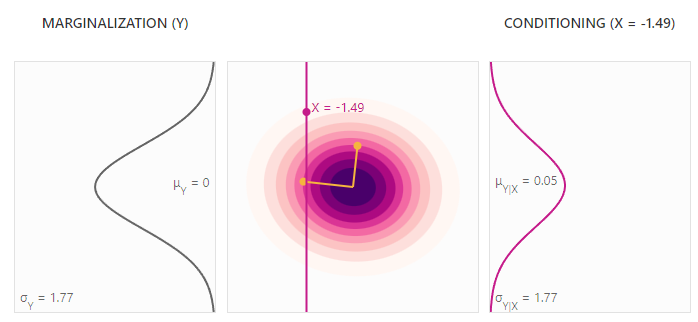
They both reduce dimensionality, but it's important to note that they are very, very different from each other. Marginalization means "regardless of this event happening, what's the distribution of another event?". Conditioning means "given that this event happens in this configuration, what's the distribution of another event?"

Bayes rule

Bayes rule is derived from the chain rule / intersection discussion:

which you can generalize to

where $\gamma$ can be anything

Now, in PGM applications, the denominator or other parts of the equation may be intractable to calculate. This is where we need to do some approximations.

The quick trick with bayes

When you have something like $P(C | A, B)$ and you need to flip the A and the C, think automatically that you need a joint distribution of $P(C, A | B)$.

Conversely, when you have a joint distribution $P(C, A | B)$ and you divide it by something on the left side of the conditional, like $P(C)$, you can imagine this “bumping” the $C$ to the right, getting $P(A | C, B)$