Laplace distribution

This is defined as follows:

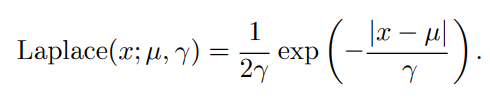
where $\gamma$ is the "constricting" factor. The smaller the $\gamma$, the sharper the peak.

Dirac distribution

If all the mass in a distribution is in a singular point, we arrive at the Dirac Delta function. The PDF of $\delta$ is infinite at $x = \mu$ and zero everywhere else, and the integral of the PDF is 1. As such, it's less of a "function" and more of a distribution

Empirical distribution

If you are given a bunch of points, the following will maximize the likelihood of the data:

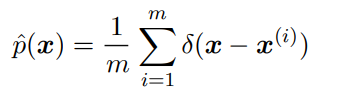
(if you think about it, it's kinda obvious)