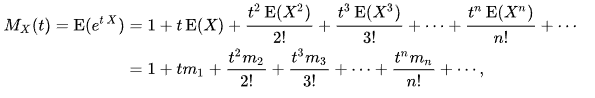Moments

Moment computation can be pretty tricky for the general case (see: moment-generating functions). However, here’s some tips

• first moment is the mean of a distribution

• second moment can be computed if the variance and the first moment is known, as $Var(X) = E[X^2] - E[X]^2$.

Moment-Generating Functions

Here’s the problem: given some random variable $X$, what is the $n$th moment of $X$? The first moment is the expectation and the second moment is the variance, but this is not sustainable for higher moments. Instead, we find a general formulation.

🐧 Definition of MGF

Define some function $M_X(t)$ such that

Now, because of the taylor expansion of $e^{tX}$ and the linearity of expectation, if you differentiate $M_X(t)$ $n$ times and set $t = 0$, you get the $n$th moment

• Proof (taylor)

  

Uses of MGF

The main uses of MGF is to find the $n$th moment. But there are other uses too

• MGF uniquely determines distribution

• MGF has the unique ability to move you between the expectation of an exponent of an RV to something without an expectation. Keep this in mind!

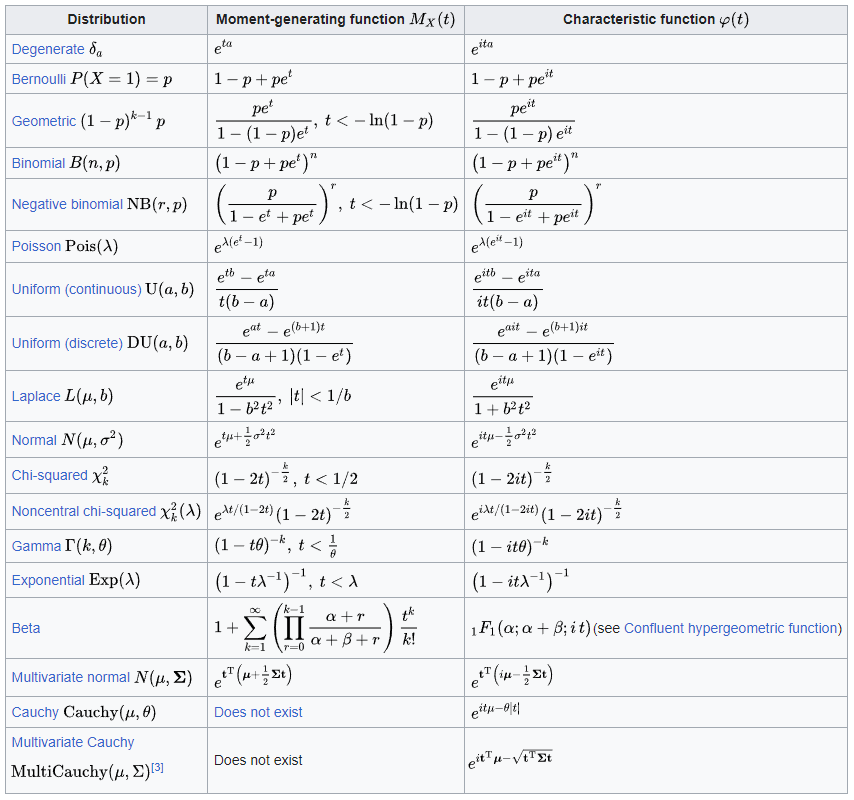
Common MGF’s