Importance Sampling

Importance sampling allows you to compute an expectation under a distribution using samples from another one, as long as you can evaluate under the original distribution.

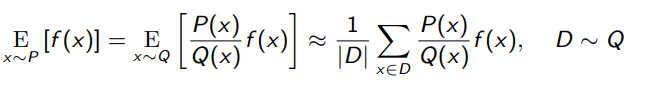
We call $P(x) / Q(x)$ the importance sampling weight. Now, a key restriction is that the support of $Q$ must be larger than $P$, or else you will run into a divide by zero.

Intuitively, importance sampling is just pinching a distribution to make it into a different distribution. Importance sampling is unbiased, but it is high variance.

Variance of importance sampling

We can compute the variance

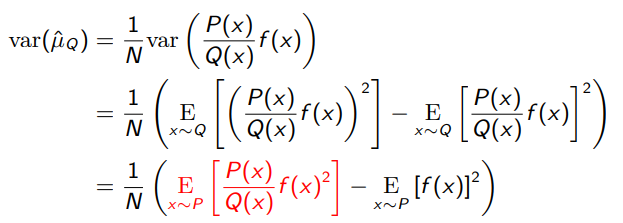
and this trick is just we push it back into the original distribution, but the squaring effect has an unfortunate residual. If there are any situations where $P(x)$ is likely but $Q(x)$ is not likely, then this $P(x)/Q(x)$ term can explode. Therefore, the variance is very unstable and can be quite large.