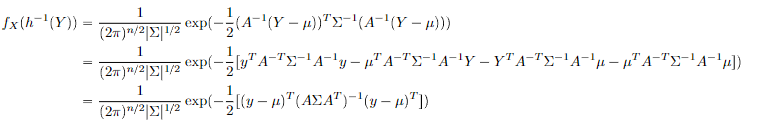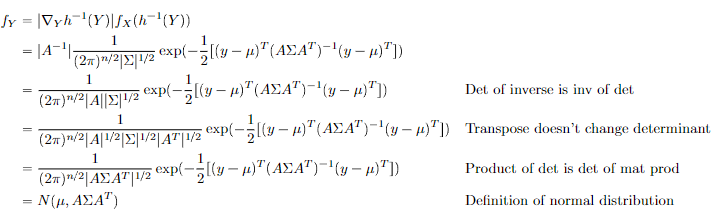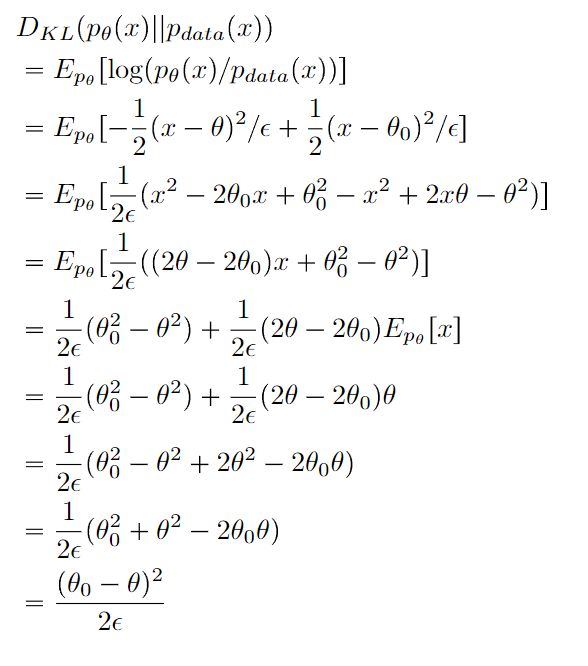Gaussians

The formula

Properties

• Sum of independent gaussians is gaussian (proof through convolution)

• Affine transformation $Y = Ax + \mu$, if $x \sim N(0, \Sigma)$, then $Y \sim N(\mu, A\Sigma A^T)$
  • Correllary: $aN(\mu, \Sigma) = N(\mu, a^2 \Sigma)$ for a scalar.

• Proof

  Standard distribution mapping objective

  

  

• The KL divergence of two same-variance gaussians is simply the scaled square distance of the means

• Proof (just expanding the definition)

  

Transformation

The “folded gaussian”, or $|N|$, is the Chi-squared distribution. This can be helpful when dealing with norms of gaussian samples.

Sub-gaussian

When we have a sub-distribution, we are talking about the decay of the tails. Therefore, a sub-gaussian distribution has tails that decay at least as fast as the tails of the gaussian. More formally, if for every $t \geq 0$, we have

then we have sug-gaussian properties.

Sub-gaussian distributions can be upper bounded by the gaussian tail bounds, which can be nice. There are some more complicated properties of distributions here that we won’t necessarily get into here.