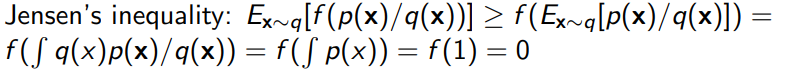KL divergence

KL divergence is an asymmetric measure of distribution separation

• Decomposes to log likelihood in certain situations

• Two very different objectives depending on which way you write the KL divergence

F-divergences

Given two densities, we define a general f-divergence as

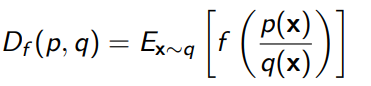
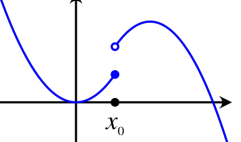
where $f$ is any convex, lower-semicontinuous function with $f(1) = 0$. Lower-semicontinuous basically means that around $x_0$, every point that is below must be continuous. Every point above is fine. This looks like the following diagram:

Properties of F-divergences

Always greater than zero

• Proof (convexity, Jensens)

  

Examples of F-divergences

There are so many types of F-divergences, with a common type being KL divergence, where $f = u\log u$ (careful! It’s not $\log$ because it’s $p \log p/q$, not $q \log p/q$. ) Total Variation is also a common one, where the $f = |u-1|$