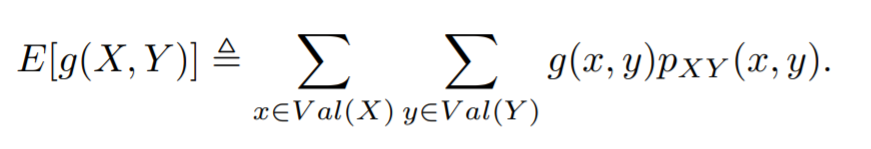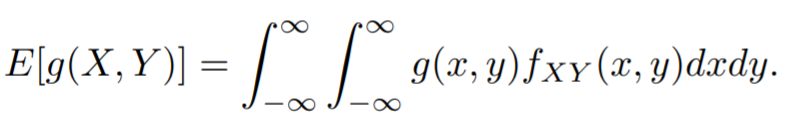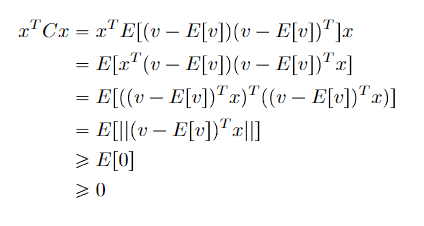Covariance

Tags

Covariance of two RV’s

Expectation of two random variables are defined as follows:

Covariance of two random variables are defined as follows:

☝

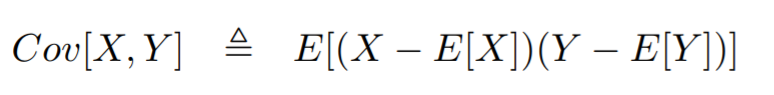
High magnitudes of the covariance means that the values are very correlated in a linear fashion. A zero covariances does NOT mean no correlation; it can be non-linear.

Important identities to know

expectation is still linear

$Var(X + Y) = Var(X) + Var(Y) + Cov(X, Y)$

Independent $X, Y$ means that $Cov(X, Y) = 0$ ( but it's not a bidirectional relationship)

Covariance matrix

A covariance matrix is a matrix that contains pairs of random variable, and it is symmetric. It is defined as the following:

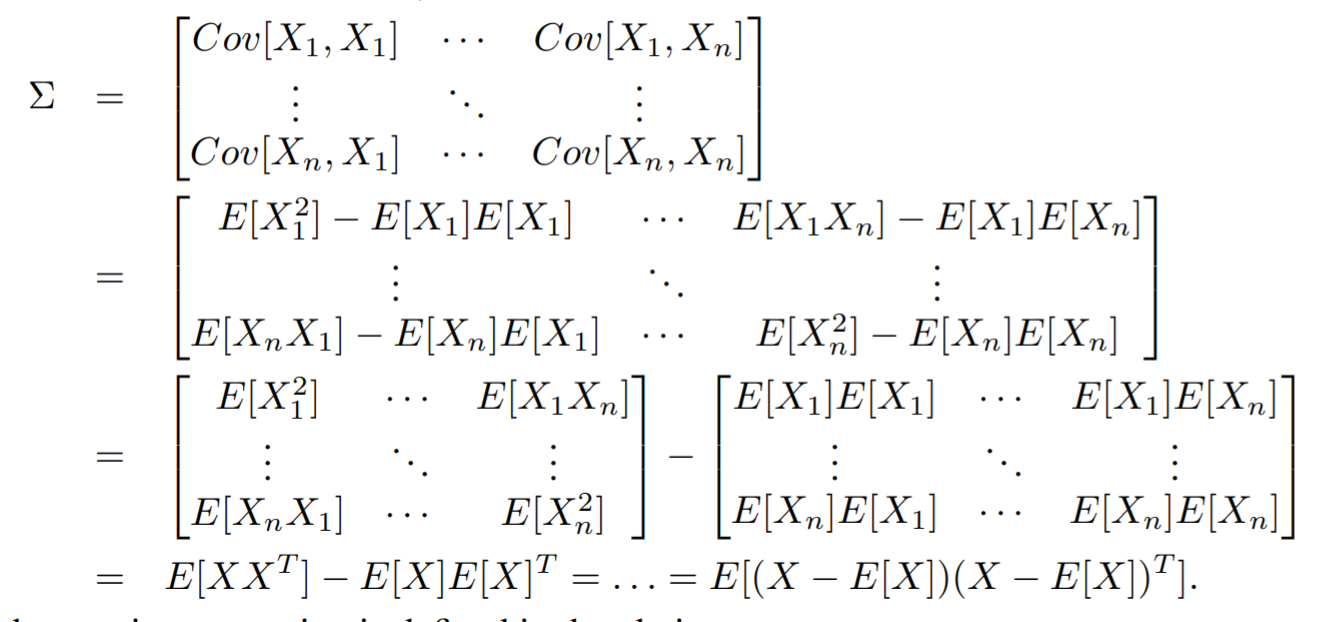
Furthermore, it is also positive semidefinite (partially because variances can't be negative)

Covariance in expectation

💡

Use this to improve the probability notes

Now, we can make a covariance matrix $\Sigma$ such that $\Sigma_{i, j} = Cov(X_i, X_j)$ . This is how you deal with variances in vectors.

Using element analysis, we get two equivalent forms:

C = E[(X - E[X])(X-E[X])^T] = E[XX^T] - E[X]E[X]^T

So you can see that vector covariance has the same form as scalar variance!

🚀Covariance Matrix is PSD

The covariance matrix is positive semi-definite, which can be helpful for derivations of convesity

Proof (PSD definition that yields a norm inside expectation)