Tricks with marginals and complexity
| Tags | CS 228Inference |
|---|
This is something that is a little confusing to me, so I thought I would dedicate some writing to it
Marginalizing only part of a set
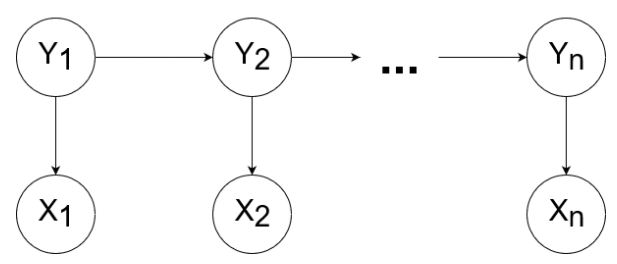
Let’s say that you wanted , which means that you need to marginalize out all Y’s from . When doing this, don’t worry about where the X’s end up! Only worry about where the intermediate Y’s end up! Because here’s why: you will eventually be removing all from the distribution. So any large cliques you make, you will have to deal with them eventually.
This idea is nice and intuitive: when marginalizing, the largest clique you form is the complexity it ends up with. and in fact, that’s all you need to know. A clique of size will take time to marginalize.
But let’s try to understand this at the point of maximum confusion.
Cliques vs chains
Cliques
Cliques of size are represented by factors with elements. This takes time to marginalize out.
When you want to marginalize , where each variable has values each, then you need operations. You can think about as a table that requires elements to convey the whole data. It’s helpful to think that every time you make a clique, you must write out the tabular for it. (this intuition prevents you from backpropping too far)
Chains and dynamic programming
The key to understanding chains and dynamic programming is to separate the creation of the factor and the accession of the factor

Let’s look at the message passed to , . This is a table of elements, but each element takes time (summed across ) to make. Therefore, to construct the , we need . But here is where the dynamic programming comes in. We cache this such that all future uses will be When we create , we need to marginalize . However, this is not the bottleneck. Rather, it’s the that causes the next to also be constructed in time. Memoization breaks the recursion early.
As such, these chains also obey the clique rule. The cliques are of size 2, so they must run in time each.
Multiple ways of interpreting the same problem.
Special shapes
Square grids
To marginalize out a square grid of size , you start in the corner and move your way down an edge. However, you will realize that at the end, you end up with the next edge being an -clique (see this for yourself). Now, as you start plucking away this edge, you will see that this -clique stays the same (remove one, add one). Therefore, the complexity is , as you have to do the removing operation times with complexity each time.
Why every time? Well, you imagine making the new factor. This requires you to fill a table of size