Converting Bayes

The key insight is that while MRF’s are less intuitive to understand, inference algorithms can run easier on them. Therefore, it is often better to convert a bayes net into an MRF.

Key observation

Bayesian networks are just a special case of MRF. Take this, for example

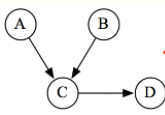
You have $P(A)P(B)P(C | A, B)P(D | C)$. The first three can be turned into a factor $\phi(A, B, C) = P(A)P(B)P(C| A, B)$. The last one can be a factor by itself: $\phi(C, D) = P(D | C)$.

As such, we come to understand that any parent-child relationships should be turned into a clique, and the associated factor is just the products of the parent-child relationships in the Bayesian network.

Moralization

We will now formalize this observation. We define the moral graph of an original Bayes network $G$ as an undirected graph that contains an undirected edge between $X_i, X_j$ if

1. there was originally a directed edge in $G$ between them, in either direction

2. $X_i, X_j$ are parents of the same node.

We call this process moralization, which mean “marrying the parents”

When we moralize edges, we lose independence information. For example, when we moralized the above relationship, we lost the independence $A\perp B$.

Going the other way around

this is more complicated but it can be done. You pick a root node $A$. Then, you establish the children $B, C$. But then, you ask yourself, is $B\perp C | A$, and this is no. So you must add another edge. You pick another node as a parent, like $B$. This gets you children $C, D$, and you do the same test. You keep on doing this!

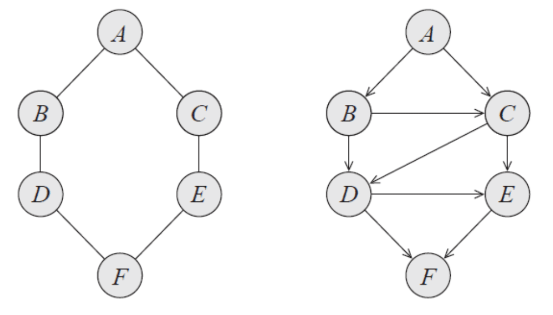
In general, turning MRF into bayes requires a chordalizaiton of the graph. Pretty neat!

But no free lunch

So is it the case that for MRFs, can we express everything that Bayes nets can? Actually, no. In fact, the simplest directed phenonemon, the V-structure, can’t be described by MRF. In this particular case, we struggle to show that $X$ and $Y$ are independent because nothing is observed and there does exist a path between $X$ and $Y$ in the MRF.

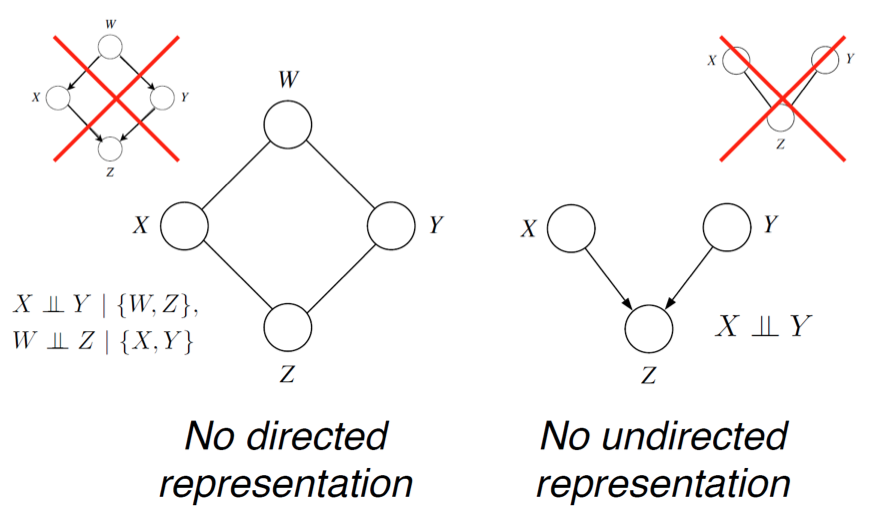
More specifically, connected MRF’s can’t represent unconditional independence. It’s a little weird that way.

So the upshot is that neither model is perfect. Here’s a nice chart that shows how graphs and the statistical properties of the two models relate.

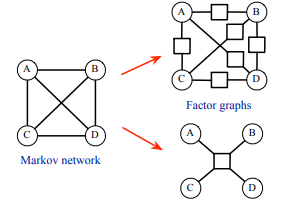
Factor graphs

In MRF, we didn’t explicitly represent the factors which got a little confusing. To make things more explicit, we make a different type of graph that has both varaible vertices and factor vertices, like the one shown below.

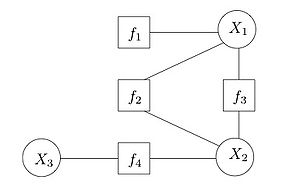
You can decompose an MRF into different factor graphs, depending on the context