Conditional Models motivation

When you have a PGM, you often want to do something with it that involves observing something and then using that observation to create something else

In previous classes we talked about generative vs discriminative models, and now we can formalize it. These two models are technically I-equivalent, so they do encode the same independencies. However, they each have their own benefits and drawbacks

Generative models

In the generative model, the $Y$ influences the observed $X$. Because it is generative, you necessarily need the entire joint distribution. So you need $P(Y)$ and all forms of $P(X_k | Y, X_{PA(X_k)})$. Eventually, you will get $P(X_1,..., X_n, Y)$. From this, you can make all sorts of inferences. For example, if you divide by $P(X_1, ..., X_n)$ you can get $P(Y = y | X_1, ..., X_n)$.

The pro, again, is that we have the joint distribution at hand.

The massive con is that the joint distribution can be horribly complicated (think about how we would represent $x_n$ in the above graph!

To simplify, we often make additional independence assumptions. For example, in Naive Bayes, we assume that every $X_i \perp X_j | Y$, which removes the densely connected children edges.

You would calculate the conditional probability in a Naive Bayes setup like

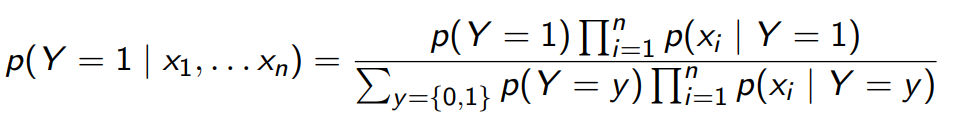
Discriminative Models

Ok, so why don’t we try something different this time? What if we drew arrows in the other direction?

In this case, there are a crap ton of variables influencing $Y$, so we can’t make a tabular look-up that we would have done for the naive bayes. Instead, we make this assumption:

where $f$ is a valid probability. In other words, we can represent the dependencies as a function. hmmmm. This should sound rather like regression!

In fact, we can try the following:

This is just logistic regression.

What are we assuming?

It seems like we just got free lunch. In Naive Bayes, we were only able to make a tractable conditional inference when we made the conditional independence assumption. Why is it easier here?

Well, there’s one crucial thing missing. Because the $P(Y = 1 | X_1, ... )$ was directly accessible from the model (without using Bayes rule), we had no need to calculate $P(X)$. Without $P(X)$, we don’t have the joint distribution.

Therefore, the generative models can do many things because it is a joint distribution, while the discriminative model is relegated to calculating $P(Y = 1 | X_1, ...)$. So in not giving up the dependencies between variables, we had to give up the joint distribution.

The assumptions also come with the choice of $f$. For example, in the logistic regression above, we are assuming implicitly that the data is linearly separable.

When discriminative and generative intersect

It can actually be shown that if $P(x_i | y)\sim \mathcal{N}$ in an IID fashion and $p(y)\sim Ber(\pi)$, through bayes rule we arrive at the fact that $P(y | x_1, ... x_n)$ is in logistic form. We did this in 229.

So this reinforces the no free lunch idea. The predictive power of these two models are equivalent.

Compare and contrast

Discrimination cons

What if we are given partial observability of the $X$? With the generative model, it is fine as we can marginalize across the unknown values to give our best guess. However, the discriminative models are dead in the water because the key assumption is that it observes all of the necessary variables.

What’s more, because discriminative models are typically trained through gradient-based methods, it often needs more data.

Discrimination pros

The key power of discrimination is that it doesn’t make any assumptions about $X$. Sometimes two features are very closely correlated (think “bank” and “account” in an email). Therefore, the conditional independence assumption may not be correct and we can underfit.

On the other hand, if the discriminative model sees two correlated features, it will learn to ignore one of those features. Or, at least it is capable of learning this ignoring, while the generative models can’t.

Conditional random fields

Previously, we looked at models where $Y$ was a single value and $X$ as a set. Can we make things larger now with $Y$? What if we had many $Y$ and many $X$?

A good example is below

we want to predict letters given a series of images.

This is still a discriminative model because we don’t want to find the distribution $P(x)$. We just want to find $P(y | x)$ and maximize the $y$ to make a prediction.

Intuition

This is a weird thing. $P(y | x) \propto \prod \phi(x, y)$. This is because $p(y | x) = p(x, y) / p(x)$, but $p(x)$ is a constant. This denominator is actually known as the partition function , and that’s why its known as a “function”. However, if you want a non-normalized distribution, you can just take the product of factors.

Formalism

This is the third class of conditional models that we didn’t talk about yet. We have a set of variable $X$ and $Y$, and we define the conditional distribution as

Note how the cliques include both $X$ and $Y$ now. It is possible to have cliques in this product that don’t have both. For example, in the handwriting graph, we need $y$ to $y$ connections.

We define the partition function as

This is because we observe $x$, but we must make the distribution of $y$ legal.

Intuition

First, you can think of a CRF as a normal MRF except that we have a set of variables already observed. Therefore, you can make some conclusions about which variables are independent using the graph separation.

Second, you can think of the CRF as a joint distribution with a slightly different sum. A normal joint distribution sums to 1 across all variables. A conditional distribution also depends on all the variables, but it sums to 1 across only the variables that are not conditioned . This is why we modified the partition function.

Definition of factors

Just like in discriminative models that, we find that our factors may become intractable. For example, in the handwriting graph we need to compute $\phi(x_k, y_k)$, which is a map between an image and a letter. No tabular form will work! Therefore, you can use a parametric model, like a convolutional neural network to work as the factor.

And here’s something important: because we are always observing x, we don’t need to worry about modeling $p(x)$! Therefore, you can use a complicated feature distribution without worrying about modeling it. But of course, it means that we don’t have the true joint distribution on hand.

This is a little tricky so think about it for a second. A conditional probability distribution is also a function across all variables, but unlike a joint distribution, these conditional distributions only are “active” on the unobserved variables.

CRF and logistic regression

Once again, we can show that logistic regression can be derived from CRF. Let’s look at this graph

If you let $r(y) = \exp(\alpha_0 1_{\{y = 1\}})$ and $f(x_1, x_2, x_3, y) = \exp((\alpha_1x_1 + \alpha_2x_2 + \alpha_3x_3)1_{\{y = 1\}})$, then we get

And the normalization constant is just

When you put this together, it is just the logistic regression!

CRF pros: summarized

1. no dependency encoding with $x$, which allows a large set of observed variables without worrying about their dependencies

2. allows continuous variables

3. incorporates domain knowledge with the graph structure