Independence in a Bayes net

We will define $I(p)$ to define the set of variables that are independent in a bayes net.

The general rule

Here’s a general, powerful rule. When conditioned on its parents, a variable $X_v$ is independent from all of its non-descendents.

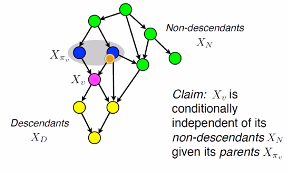
• Proof

  First proof relies on content taught below. Essentially, if we look at the non-descendants immediately adjacent to the parent, we can form a triple with the parent in the center. We know that this triple is not a V-shape, because then the child would point to the parent. Therefore, it must be one of the other cases. In this case, because the parent is observed, there is no active path between the child and the non-descendants, meaning that it is independent.

  The second proof relies on a fun trick of algebra.

  We want to find $p(x_v | x_{\pi_v}, x_N)$ where $\pi_v$ is the parent of node $v$. We do this by bayes rule, as shown below

  

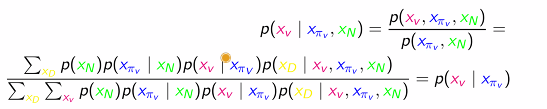
This is a local independence. We can also talk about global independence by means of d-separation.

Conditional independence in elemental building blocks

Bayes nets can be looked at in running triplets, with two distinctive behaviors.

One type decouples two variables through observation of the other, while the last type will couple two variables through observation of the other

Cascade

In (a), we see $X → Z → Y$. Using the general rule we described above, we claim that $X \perp Y | Z$. However, it is NOT the case that $X \perp Y$ in general. This actually makes a lot of sense. Let X = oil catches on fire, Y = house catches on fire, and Z = firefighters arrive. When conditioned on the fact taht the house caught on fire, “knowing” that it was an oil fire doesn’t influence much of the fact the firefighters will arrive. However, if we don’t condition on Y, then when oil catches on fire, it is strongly correlated with firefighters arriving.

We can think about this graph business as the flow of information. If we catch the immediate source, anything upstream doesn’t really matter.

Common parent

In (c), we see that $X \leftarrow Z → Y$, which means that $X \perp Y | Z$. Again, we can understand this in terms of information gain. If $Z$ is “house on fire” and $X$ is “firefighters arrive” and $Y$ is “people exit the house”, then once we know that the house is on fire, knowing X or Y doesn’t inform the other very much. On the other hand, without knowing that the house is on fire, firefighters arriving gives a lot of correlation to people exiting the house

V-structure

In (d), we have $X → Z \leftarrow Y$.

This one is a little tricky because it’s the exact opposite of what we see in the other cases. In particular, $X \perp Y$ when $Z$ (or its descendants) are not observed, but $X \not\perp Y | Z$. Why? Well, let’s say that $Z$ is true. If we observe that, and we also observe that $Y$ is true, then this $Y$ “explains away” why $Z$ is true, and therefore $X$ is less likely. None of this happens if $Z$ is not observed.

What about the children / descendants??

this is a very interesting question. So if we had something like $A \leftarrow B \rightarrow C$ and we observed a child of $B$, say $D$, does it break the original ABC?

The answer is NO! Let’s say that $B$ is “going to college” and $A$ is “reading well” and $C$ is “writing well” and $D$ is “speaking well”. If we observed that someone is speaking well, it makes intutive sense that we can’t suddenly make reading or writing independent. The original variable $B$ is the only variable that can make all three $A, C, D$ independent from each other.

The only time that this rule is broken is on the V-structure. In $X → Z \leftarrow Y$, if any child or descendant of $Z$ is observed, then $X$ and $Y$ is dependent. Using an example we will develop below, if we have a child $W$ = “firefighters come,” ( a result of your house being on fire), then knowing that you had a kitchen accident will still explain away the fire and subsequent firefighters. This is because the two parents of $Z$ forms a cascade with any of Z’s children, while in the previous examples, this is not the case.

Explaining away

Here’s some more important information about the V-structure. This one is definitely the oddball because learning more will couple two independent variables. This is the principle of “explaining away”, and it is a very important one to understand.

Here’s a helping example: Let’s say that $Z$ is “house on fire” and $X$ is “kitchen accident” and $Y$ is “electrical accident.” Normally, X and Y are independent. However, if we look and see that the house is on fire and we also know that there was a kitchen accident, the the likelihood of Y being true is less because $X$ “explained away” the phenomenon.

The idea of observation

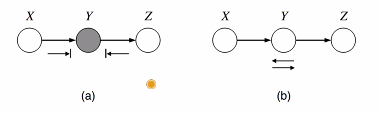
This is more of a philosophical look into what it means to observe a node and why it disrupts certain dependencies. In the non V-structure atomic structures, some sort of information is passed through the triplet. In the cascade, the head of the cascade influences the next in line, and so on. And the information flows both ways because if the tail is affected, it gives us information about how the head behaves.

So in some ways, it’s worth thinking about dependence as a passing of information. Before observation, information flows through the path unhindered. As in, when we observe the tail, we can get new information about the head.

But once we observe in the middle of the cascade, we’ve already “peeked” at the information, effectively spoiling its novelty. Now, when we observe the tail, we can’t get any new information about the head because the middle already gave it to us.

The same mode of reasoning applies for the V-structures but in reverse. Prior to observation, knowing one side doesn’t give us any more information about the other side. But once we observe the center, then when we know one side, we know that the other side probably has less of the desired trait.

Markov Blankets in a bayes net

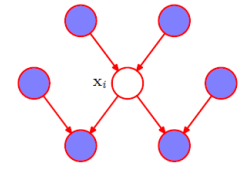
No matter how complicated the network is, as long as you observe the parents, the immediate children, and the children’s other parents, then a node $x_i$ will be independent from everything else. This is especially helpful when you want to calculate things like $P(x_i | everything else)$

Aside on observation

You can say that we observe something in a graph. Overall, this might mean that you have $A \perp C | B$. This means that you observe $B$. However, in an intermediary calculation to perhaps arrive at this result, you don’t take this observation as granted. You might calculate $P(A, C | B)$ but if you use an intermediary calculation $P(C, B | A)$, then you aren’t observing $B$ anymore! You are observing $A$!