D-Separation

The cool part is that we learned all that we need to know about bayesian structure because these three patterns form the recursive building blocks for all other bayesian networks. To do this,

But to understand this, we must first understand D-separation. Intuitively, it’s just a generalized concept of conditional independence that we use to describe between sets of variables and not single variables any more.

Formalism

Three sets of nodes $Q, W, O$ are considered D-separated given $O$ if $Q$ and $W$ are not connected by any active path. What does that mean?

Active path

In an active path ( a list of nodes), at least one must be true for ALL consecutive nodes on the path

1. $X → Y → Z$ or $X \leftarrow Y \leftarrow Z$ and $Y$ is unobserved (i.e. not in $O$)

2. $X \leftarrow Y → Z$ and $Y$ is unobserved

3. $X → Y \leftarrow Z$ and $Y$ or any of its descendants are observed

This is just a fancy way of saying that the information propagates through the path freely. In other words, the all the variables in that path are dependent on each other; it “passes” dependence and nothing ruins it. When we say “ruin”, we mean observation in some cases, or non-observation in others (see discussion on information passing in other section)

For example, if $Y$ had been observed for 1 and 2, then $X$ and $Z$ become independent, and therefore $X$ becomes independent of everything after that $Z$; the chain is broken;

D-separation in terms of active paths

Back to D-separation: because we DON’T want an active path, it is quite easy to show D-separation. Just find/make a counterexample for every possible path through the graph.

• Example (very helpful)

  This may be a little difficult to wrap your head around, but essentially there exists no active path between $X_1$ and $X_6$ when conditioned on the set $O = \{X_2, X_3\}$. This is because we have a standard cascade between $X_1$ and $X_6$, and in both of these cases, it is blocked by the observed set.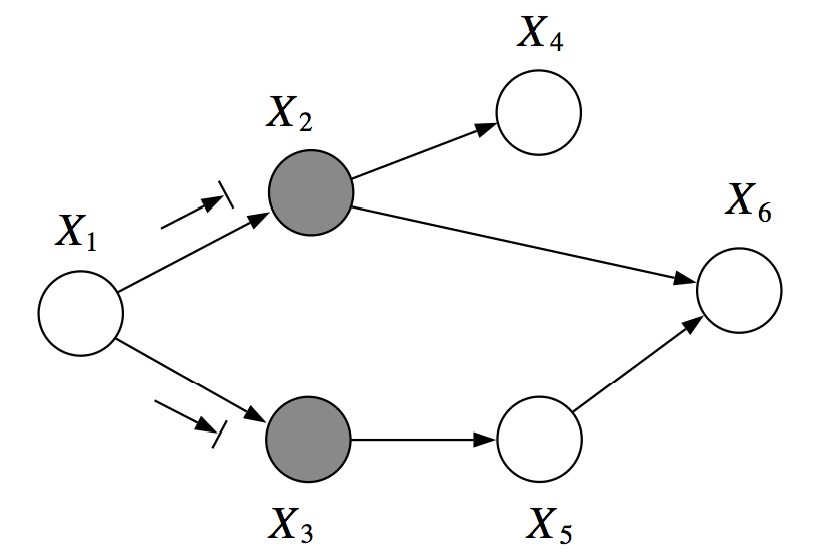

  

  However, if we choose a different observed set $O = \{X_1, X_6\}$ and look at $X_2$ and $X_3$, these two are not D-separated

  

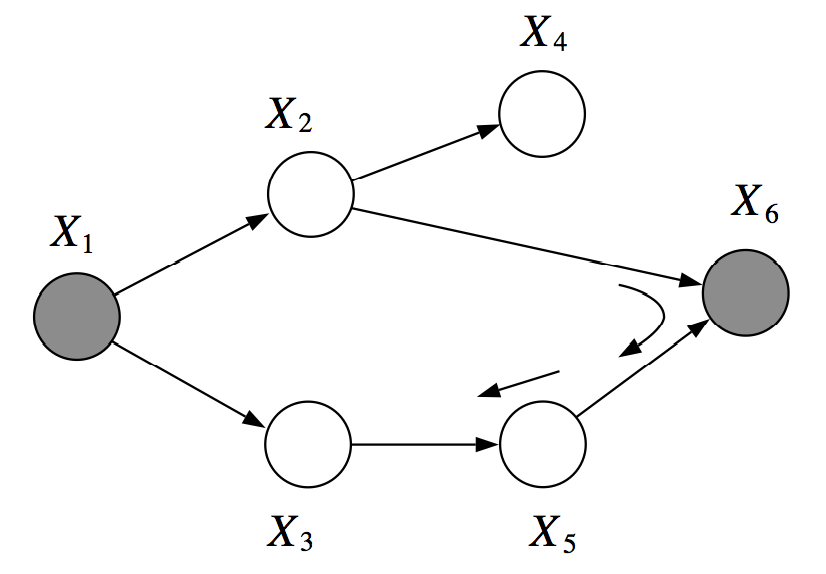
  Why? Well, there exists a V-structure between X2 and X5 that is enabled by the observation, and there is a cascade structure with X5 non-observed that completes this active path. Note that X6 being observed doesn’t influence the cascade.

• Example of observed children on D-separation

  

  In this case, G and E have an active path given B and I, because I is a descendant of H.

The general algorithm

If you wanted to see if $X \perp Y | Z$ where $X, Y, Z$ are general sets of variables, then we need to see if each element of $X$ is pairwise independent from each element of $Y$ given $Z$. To do this pairwise comparison, a BFS is the best deal

The indented bullet point needs some clarification. At every node, you check if things are blocked. Blocked means two things: if you reach a V structure and this node is not in W, or if you are not in the middle of a V structure and it is in Z. If either of these cases are satisfied, this current path is no good.

Soundness and Completeness of D-seps

We want to use D-separation to encode independencies in the original distribution $p$ that $G$ was generated from. Can we do this?

I-maps

In general, when we talk about $I(P)$, this is the set of variable sets that are conditionally independent of each other in a distribution (can be a huge set because it is a subset of a superset)

Let’s define a similar thing for a graph:

In our case, $X, Y, Z$ are all sets of nodes (can be the empty set). As such, $I(G)$ contains all the sets of nodes that are conditionally independent or marginally independent (if $Z$ is the empty set)

We call this $I(G)$ an I-map of $G$.

Soundness

It is true that $I(G) \subseteq I(p)$. Let’s take this statement by faith right now.

This actually has a pretty significant upshot: any d-separated set of nodes will be independent from each other in the actual distribution!

Completeness

However, it is not the case that $I(G) = I(P)$. In other words, there can be independences that are not captured through the D-separation approach. And, to be more big-picture, these are the independencies that are not captured in the graph itself.

Why is this the case?

While it seems counterintuive at first, it’s actually pretty straightforard why d-separation is not complete. Think about how we claimed that every distribution can be expressed as a fully-connected network? It’s because some of the arrows don’t actually do something. In the table, if the table looks like this

you conclude that $B$ is independent from $A$. And yet, in the graph, $A$ is still directed to $B$, so there is no way to tell, structurally, that there is an independence. The moral of the story is that D-separation cares about the structure, but the structure of a Bayes net only tells half of the story.

The critical upshot is this: graphical models can add dependencies where there are none, but they can’t take away dependencies. That’s why it’s sound but not complete.

Representational power of directed graphs

Almost-completeness

The good news is that, although D-sep is not complete, it is almost complete. For example, it may be that case that $X \perp Y | Z$ in $p$ doesn’t imply d-separation, but if all distributions that factor over $G$ are independent in this way, then it must be the case that $X$ and $Y$ are D-sep given $Z$. In other words, if the structure forbids dependencies, then D-separation comes automatically because it looks at the structure.

The contrapositive, therefore, is also true:

Theorem: If $X$ and $Y$ are not d-separated given $Z$, then there exists some distribution that factorizes over $G$ such that $X$ and $Y$ are dependent given $Z$.

Looking at the chart above, you see how it’s only an edge case that decouples $A$ and $B$. If you change any of those numbers (i.e. make a new distribution with the same graphical factorization), $A$ and $B$ become dependent.

Do perfect maps exist?

Is it possible to make $I(G) = I(p)$? This would be known as a perfect I-map, or a P-map. Well, it’s actually not possible to always find $I(G) = I(p)$. Take the noisy XOR example

• Noisy XOR example

  Let $X, Y \sim Ber(0.5)$. Let $Z = X \text{ xor } Y$.

  Now, we note that $X \perp Y$ by design, but also that $Z \perp Y$ and $Z \perp X$. This is because regardless of what $X$ or $Y$ is, there is an equal chance of getting either 1 or 0 (that’s the power of the XOR). But also as a result, we have $Z \not\perp \{Y, X\}$ because if you know both X and Y, you know Z exactly.

  We can factor this into $X → Z \leftarrow Y$, but it doesn’t take much thinking to see that $I(G) \neq I(p)$. There are far more independences of $p$ than $G$ expresses. For example, in $G$, it is not true that $X \perp Z$.

  So this is an example that shows that some joint distributions can’t be expressed through a graph that has the exact same independencies. And yet, the graph factorization will always be sound, just not complete in its independencies.

In fact, it’s just impossible to express that noisy XOR in its glory at all, using a Bayes framework.

Minimal I-map

A minimal I-map is the closest we can get at times to a P-map. This is when you have some graph $G$ such that if you remove any edge, $I(G’) \not \subseteq I(p)$. In essence, you have the slimmest graph possible given the distribution.

I-equivalence

We compare I-maps of two graphs by doing an element-wise comparison. We call two Bayes nets $G_1, G_2$ as I-equivalent if $I(G_1) = I(G_2)$

Interestingly, two I-equivalent graphs may not be unique. For example, $X→Y$ and $X \leftarrow Y$ form different graphs but have the same (none) independencies.

Therefore, P-maps also are not unique.

I-equivalence and triplets

In fact, we might have observed something interesting.

In (a, b, c) of these graphs, the variables have the same independencies. Namely, that if $Z$ is observed, the other two variables are independent. As such, we can freely change the directions of the arrows AS LONG AS we don’t make a V-structure as in (d). This V-structure is unique and can’t be changed.

The key upshot is that independence, minus the V-structures, do not care about arrow directionality!

Therefore, there exists many, many different maps with the same independencies. Or, to be more precise: if $G, G’$ have the same skeleton (ignoring the arrows) and the same number of V-structures, then they are I-equivalent.

Intuitively this is true because two graphs with the same skeleton and the same V-structures will have the same D-separations.

Although it is important to be careful about the direction of logic. I-equivalent BN’s will have the same undirected connections but the converse doesn’t hold due to V-structures. Similarly, if two graphs have the same undirected connections and same V-structures, then they are I-equivalent but the converse doesn’t hold. Here’s a counterexample. Basically, the idea is that the v-structure is short-circuited by another edge, so it doesn’t matter where it is.

Examples of I-equivalence

These two networks do not have the same I-maps because the number of V-structures are different

A review of vocab and notation

1. An active path is a path that preserves “information” along the entire path. In other words, the “dependency” travels down the path unhindered.

2. Two sets of variables are D-separated if they have no active paths between them

3. The I-set contains all the sets of nodes that are D-separated (i.e. independent)

4. This I-set is $I(G)$ or $I(p)$, and the set contains propositions. For example, $X \perp Y$ is a proposition. It can be true or false. If X is truly independent of Y in $p$, then we say that $X \perp Y \in I(p)$.

5. Two graphs with the same independencies are called I-equivalent.