Linear equations: a deeper look

We start with $y = Ax$. This is a linear equation, where we want to find some $x$ given $y$.

Overdetermined linear equations

If $A \in m\times n$, then there are $n$ variables and $m$ equations. If $m > n$, then it’s overdetermined. Therefore, for most $y$, there doesn’t exist an $x$.

Geometric interpretation: We throw a lower subspace into a higher one. Therefore, we can’t possibly cover this higher space, meaning that we can’t do the reverse.

However, can we approximately solve this equation? Geometrically, it means that we find some $x_{ls}$ such that $Ax_{ls}$ is close to $y$.

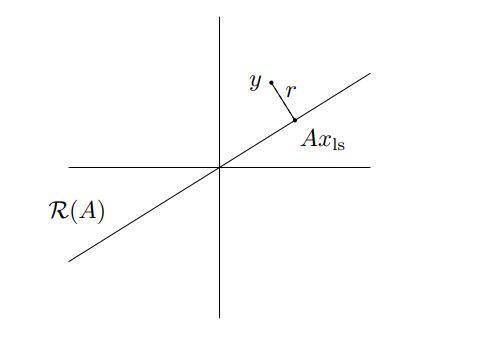
Fitting the matrix

We define the residual to be $r = Ax - y$, meaning that the norm of the residual will be

This is a quadratic form, so we can take the derivative and set it to zero

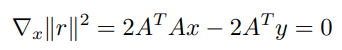
which yield the normal equations

so we get the approximate solutions as

We call

to be the pseudo-inverse of $A$. It is also the left-inverse of $A$.

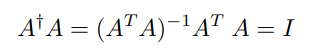
Because $AA^+$ is a matrix that projects $y$ onto $R(A)$ (think about it for a second…), we call $AA^+ = A(A^TA)^{-1}A^T$ the projection matrix.

Orthogonality principle & proof of optimality

Let’s calculate the residual’s inner product WRT anything in the range of $A$

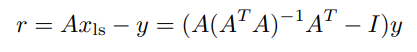
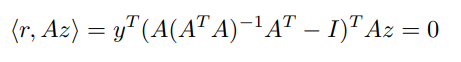
for all $z$. Therefore, the residual is orthogonal to the range of $A$. This makes sense graphically

We will now show that $x_{ls}$ optimizes the loss (we’ve already done this through the calculus, but let’s show it again, using linear algebra). We know from our previous derivation that

Using this result, we can find another meaning for $||Ax - y||^2$, which is the general “loss” function (this is different from $x_{ls}$, which is the least square that we derived. The pythagorean theorem and a little add-subtract trick yields

The best way to minimize this objective is to let $x = x_{ls}$. Neat!!

Least Squares through QR Factorization

If you can factor $A = QR$ such that $Q^TQ = I$ and $R$ is upper triangular, then the pseudoinverse is just

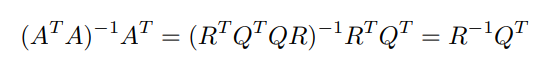
and if we project $y$ onto the range of $A$, well that’s just

Applications

Least Squares data fitting

Suppose you had $n$ basis functions, like sine/cosine (this is a special case with fourier series), but it can be anything else too. Suppose that you had data measurements $(s_i, g_i)$ and you want to fit some linear combination of functions $G(s)$ that matches the data as close as possible.

This now becomes a least squares problem, where you need to find weights $x$ such that

You can imagine a matrix $A$ such that $A_{ij} = f_j(s_i)$. The least squares fit set is

A special case of $A$ is the Vandermonde matrix, and this becomes polynomial regression.