Newton’s Method

Tags	Second Order

Newton's method

For certain tasks like linear or logistic regression, it is provably convex. As such, we can just set the gradient equal to zero and get our best solution. However, solving this equation may not be easy. As such, we use newton's method

Newton's method

Newton's method approximates zeros. The idea of Newton's method is pretty straightforward. You start with a linear approximation $y - f(a) = f'(a)(x - a)$ . By setting $y = 0$ , you get

x - a = - \frac{f(a)}{f'(a)}

As such, you perform the update $x = a - f(a) / f'(a)$ where $a$ is your previous estimate, and $x$ is your next estimate.

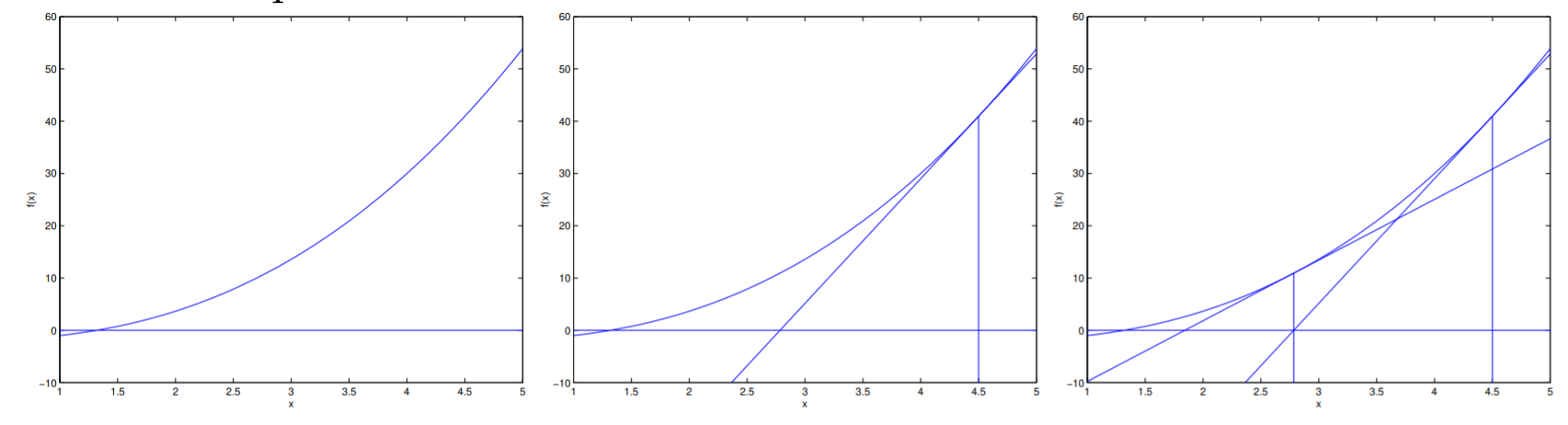
Newton's method, generalized

Instead of finding a zero on our loss function, we want to find a zero on the gradient of the loss function.

To do this, we need to find

\theta:= \theta - \frac{l'(\theta)}{l''(\theta)}

Note how we are doing exactly this—finding the zero of the first derivative.

In the vector sense, because the gradient is the first derivative and the hessian is the second derivative, we want to find

\theta := \theta - H^{-1}\nabla_\theta l(\theta)

This is known as the Newton-Rhapson method and in the context of logistic regression, it is called Fisher scoring.

You can add a weight $\alpha$ in front:

\theta := \theta - \alpha H^{-1}\nabla_\theta l(\theta)

This becomes a damped Newton's Method. It can have its advantages!

☝

There’s a close connection with Natural Gradients. In fact, it’s the same thing as damped newton’s method.

Discussion on Newton's method

Newton's method is much faster in converging than standard gradient descent. This is because it's more cognizant of the entire goal (it uses second derivatives) and will move much faster that way. It's like having a climber knowing where the bottom is, as opposed to a climber just feeling around the walls for the steepest way down.

In fact, Newton's method on a quadratic function will converge on the first step. Why? Because the gradient is linear, so a linear approximation of a zero IS the zero!

However, Newton's method isn't used that often in neural networks because these objectives are non-convex and Newton's method can actually diverge in these cases.