Matrix Calculus: fundamentals

Tags	Backprop

Gradient

☝

Symbolically,

\nabla

is the explicit gradient of a scalar function WRT to a vector of inputs. The

\partial

is a looser interpretatin. It can be a gradient or it can be a derivative WRT a matrix, etc. Keep that in mind

The gradient of a function $f: \mathbb{R}^{m\times n} → \mathbb{R}$ is defined as

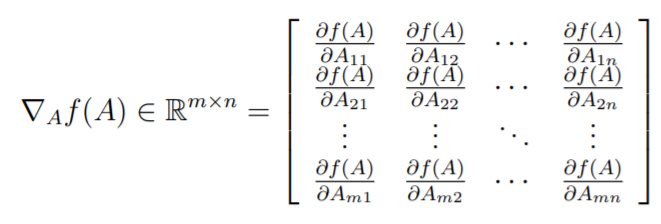
In other words

(\nabla_A f(A))_{ij} = \frac{\partial f(A)}{\partial A_{ij}}

A gradient is ONLY for functions that return scalars. Gradients are technically linear transformations because these hold:

$\nabla_x(f(x) + g(x)) = \nabla_x f(x) + \nabla_x g(x)$

$\nabla_x (t \cdot f(x)) = t \nabla_x f(x)$

Hessian

A hessian matrix just takes in a function $f: \mathbb{R}^n → \mathbb{R}$ and returns a $n \times n$ matrix that is symmetric, defined as

H_{ij} = \frac{\partial^2f}{\partial x_i \partial x_j}

Or more graphically,

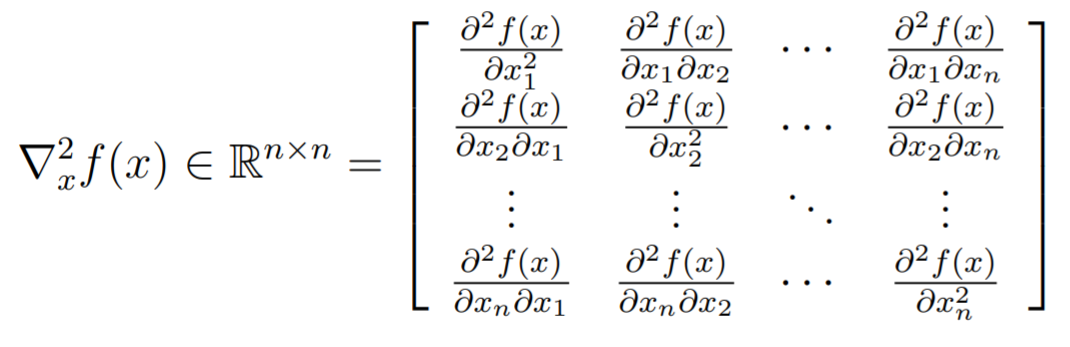
Interpretations

the hessian is the derivative matrix (Jacobian) of the gradient

each column is just the gradient of one component of the first derivative gradient [this is often the easiest to remember]

The gradient is the first derivative analogue, and the hessian is the second derivative analogue

Chain rule

Chain rule is just the multiplication of Jacobians. In the case where we try to find the derivative of a matrix, just know that a matrix isn’t a 2d thing…it can be flattened. So that’s how you get out of doing things with 4d tensors. We will talk more about this in the “practicals” section, where we learn common tricks.

Micro and Macro

You will always have element analysis. But more often than not, try to use the macro properties first, as they are often more informative