What’s wrong with scaling up?

Meta-learning deals with large computational graphs, which doesn’t scale quite well. Think about black box models: you need to roll back a lot of past model executions.

If you run MAML even on a 2-layer MLP with a large number of gradient steps, you get in excessive of 100 GB of floats in your graph!

More than just MAML or protonets—large scale meta-optimization is very important.

• Hyperparameters optimization

• Dataset distillation: can you reduce the dataset down to a few representative examples?

• Optimizer learning: can you learn a model that acts like an optimizer? Feed in gradients and other information, and output a change in weights. It can actually train itself!

• Neural architecture search: output a sequence of parameters for the best architecture for a network

Approaches

The setup

You can view all of these problems as a sort of unrolled computational graphs, in which you have a bunch of states (essentially parameters) and you have one final loss objective.

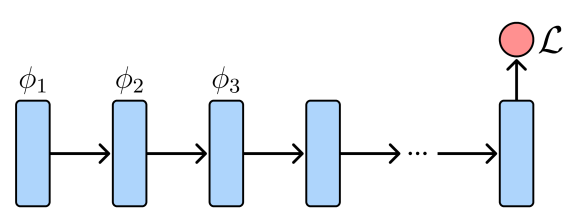
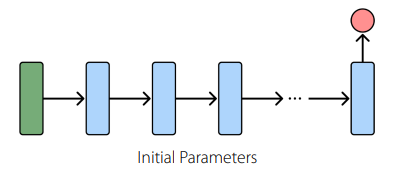
You can change initial parameters (meta-learning, MAML)

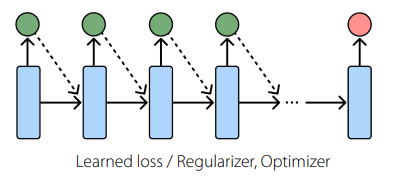
or you can have a learned loss, etc

or you can have synthetic data or even the architecture

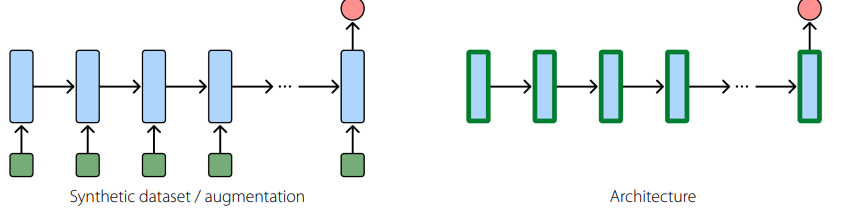
All of these things are very hard on the GPU!

Truncated backpropagation

Essentially don’t roll out the whole graph and optimize over it; only optimize over a small time window

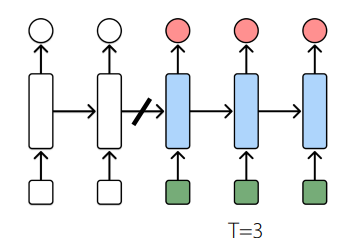
The ultimate tradeoff is bias vs computational complexity. The larger the $T$, the less biased an estimator but the larger the model.

Gradient Free optimization

Use a genetic algorithm in this outer loop! Sample “particles” in the space of parameters and let them run

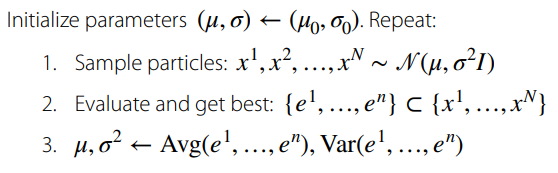
The pro is that this is agnostic to the computational graph size. It is also highly parallelizable, and it doesn’t require the inner loop to be differentiable.

However, the big con is that in high parameter complexity spaces, it is unlikely to land in a good region, even with a good genetic algorithm

Other approaches

• simplify inner loop gradients

• simplify the chain rule (essentially reduce complexity of differentiation)