Another way of doing things

What if you just took the test datapoint and compared it to the training data? It feels like a dumb thing to do, but when you don’t have enough data to work with, this simple approach might do better.

But what sort of distance metric would you use? You can’t exactly use L2 distance, especially if the inputs are images.

But there are other approaches that essentially use the idea but have a more complicated notion of distance.

The general algorithm is the same as black-box or optimization-based, but the inner loop you essentially compute $y$ directly through some similarity metric.

Siamese Networks

This is very simple: have two networks with the same parameters encode an image, and then have a head that computes the distance between the embeddings. Essentially, you’re just learning a representation and distance metric at the same time. The output is a label that predicts if the two images come from the same class.

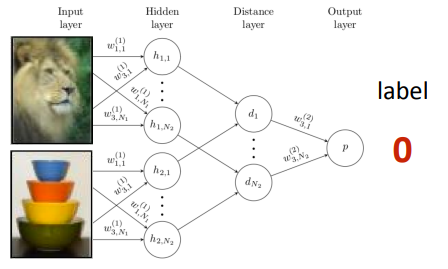
Meta-training would be to make a good siamese network through this binary classification task. Meta-testing would be to use this network and compare with the $n$ classes and give the maximum. While this is nice, there is a difference between meta-train and meta-test. Can we mitigate this?

Matching Networks & Prototype Learning

The idea is the same as siamese, but this time, meta-train and meta-test are the same thing.

You take in $D^{tr}$ and encode it in a series of $N$ embeddings (you use an LSTM to create correlations between these embeddings, as opposed to just a feed-forward for each embedding. Then, you embed the test set image and compute the dot product similarity.

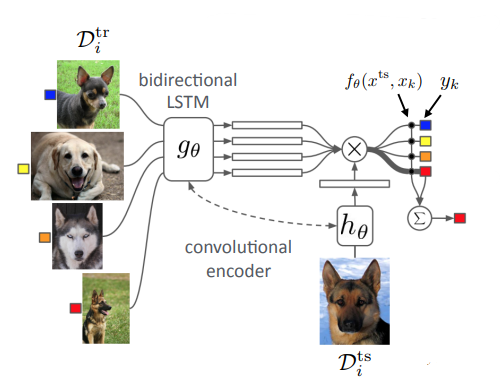
which means that your output is

where $f_\theta$ is a combination of an encoding network and an inner product.

Prototypical networks

You can understand this processs above as creating a prototype for each class, and then comparing the embedding with the prototypes. This is why it’s also called prototype learning.

For each class, you average the embeddings to create this prototype, which allows for more stability. If you didn’t do this, you might have some unpredictable behavior near the boundaries of the groups.

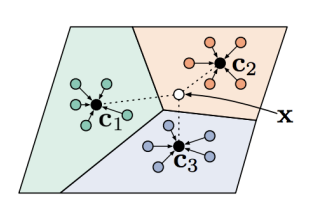
You would “soften” this prediction by using a distance metric between an embedding and a prototype. Using a softmax, you make it into a distribution

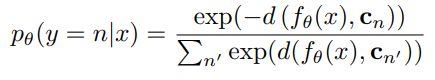
Tricks of the trade

1. self-supervised objectives as additional tasks are always good

2. more context is also good