What is domain adaptation?

There is a source domain where you have labeled training examples, and there is also a target domain. You may have labeled target domain data, partially labeled target domain data, or unlabeled target domain data. Today, we focus on the harder on, unsupervised domain adaptation.

You can think of domain adaptation as a special case of transfer learning. In domain adaptation, you can think of having the same $p(y | x)$ but a different $p(x)$.

What does this mean? Well, it means that there exists some model that does well on both the source and target; they are not contradictory. However, we don’t have good data on the target domain (in this case, no supervised data at all), and the $x$ can be very different distributions. This is what makes it hard!

While such a universal model exists, our objective is to find something that does well on target data, based on training with source data.

Examples

Some examples might include segmenting buildings using source data in a more resourced region of the world and deploying on an under-resourced region of the world. Or, it might be using a large source corpus of text, but then trying to apply the same inference algorithm on a smaller database.

Data Reweighting

Suppose that you had this distribution mismatch for the $p(x)$. Note, again, how $p(y | x)$ isn’t contradictory between the two distributions.

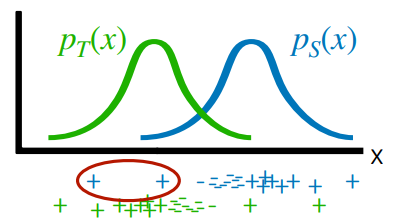
Intuitively, you can do domain adaptation by upweighting the circled points. Mathematically, we can understand it as importance sampling. We can’t sample supervised pairs from $p_T$, so we switch out the sampler distribution.

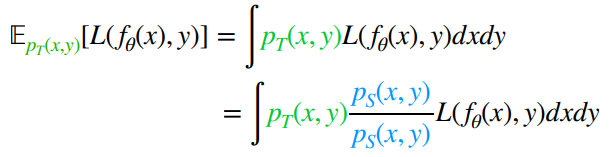
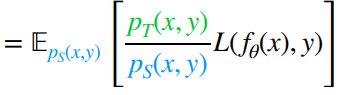
Now, this $p_T(x, y) / p_S(x, y)$ are the importance weights. By our assumption that $p_T(y | x) = p_S(y | x)$, we conclude that our objective is

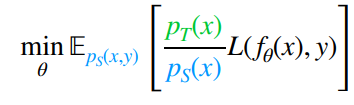
Estimating the weights

But how do we estimate $p_T(x) / p_S(x)$? An initial thought is to create a generative model that allows you to find the likelihoods. This is very inefficient. But again, anytime we are thinking of probability, think of how a certain structure gives you ways of simplifying what you really need.

In this case, we can replace our notion of separate distributions with a conditional distribution

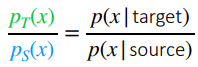
and we can use bayes rule to get

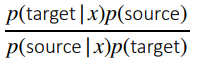
and the last term on the numerator and denomimator is a constant, so that doesn’t change things. We are left with $p(target | x) / p(source | x)$. This can be estimated with a binary classifier!

We can pretrain this binary classifier, because we have $x$ samples from both the source and the target.

Feature alignment

While weighting samples is good, there is one key problem. We are assuming that the source domain covers all of the target domain. This is not unreasonable if you are training on large source databases, but let’s say that your source was MNIST, and your target was color pictures of house numbers. Now, the prior assumption would not be reasonable.

But can we just create a new embedding space and align the features in the source and target domain there?

The adversarial paradigm

Using an encoder $f(x)$, we want to make embeddings $e_s$ undistinguishable from embeddings $e_T$. To do this, we try to fool a domain classifier $c(d = source | f(x))$.

Practically speaking, we jointly train our downstream task (label regression) and our domain classifier. There’s one tricky part about this objective though: we want to reverse the gradients as they flow from the domain classifier to the feature encoder, because they are adversarial.

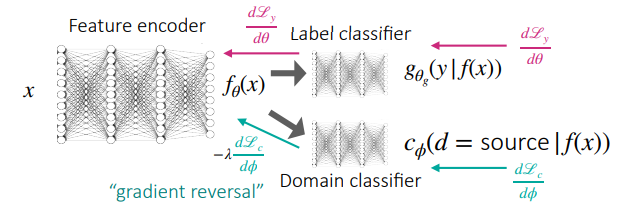
So the algorithm looks like the following:

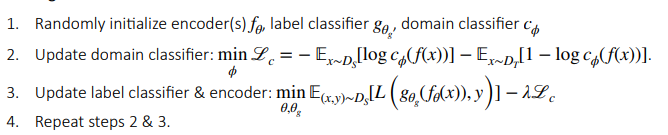
Now, gradient reversal’s optimal point for the feature encoder is to have the classifier predict “source” for every target sample, and vice versa. Actually, this is not the best! If this is true, then the samples are distinguishable after all; the classifier is just being dumb. Rather, a better objective is to maximize the confusion of the classifier. We want it to output near 0.5 for every prediction. There are more details in the original paper.

Domain translation

Instead of aligning the two domains to one latent embedding space, we can just move one domain to the other!

If you can translate source to target, just translate all source to target and train.

If you could translate target to source, just train on source and translate all target to source.

A good example is the CycleGAN, which creates functions $F: X_s → X_T$ and $G: X_T → X_S$. We have the standard GAN objective, but we also enforce cycle consistency: $F(G(x)) \approx x$. The full objective is therefore

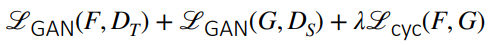
We can use this in robot learning quite well!

As a pro-tip, it is important that the label distribution match as much as possible. Otherwise, it may be difficult to find a bijection.