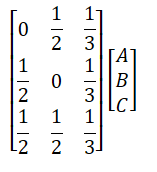Rotations

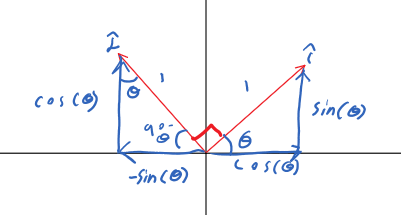
Therefore, the rotation matrix is

Rotations in $R^3$

You just need to preserve one axis and rotate the others

Rotating in x axis:

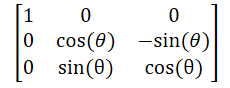
Rotating in y axis:

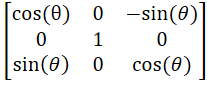
rotating in z axis;

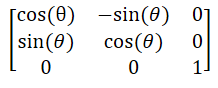
Euler matrix

An euler matrix is just a composition of rotation matrices such that when you apply the matrix to a vector, a desired rotation is made.

rotations around arbitrary axis

To do this, you just need to get a rigid transformation that rotates the arbitrary axis onto a unit axis. Let's call this $D$. Now, if $K$ is the rotation you want to make around this axis, the total transformation is $D^{-1}KD$

Reflections

You can imagine a reflection as follows: let $V$ be the subspace you want to reflect over, and let $u$ be your original vector. We know that $P_Vu$ produces a vector in $V$, and that $u - P_V u \in V^\perp$. More specifically, it's a vector that points straight out and at $u$. Therefore, the reflection across that subspace is just $u- 2(u - P_V u) = -u + 2P_V u$

Markov matrices

Markov matrices are just transition matrices whose column $n$ represents where everything in location $n$ will end up to. As an example:

In this case, 1/2 of the population in A will go to B, and 1/2 will go to C. 1/2 of the population in B will go to A, and `1/2 will go to C. And lastly, the population in C will disperse evenly across A, B, C

The key insight is that markov matrices represent markov sequences and raising this matrix to an exponent will allow us to model how a system behaves!

Gram Matrices

Gram matrices are of the form $AA^T$ and $A^TA$. they are symmetric (best thought through the dot product interpretation of matrix products) and they are invertible (see invertibility section for a proof). Whats more, they are decomposable into an eigenbasis. So, they are pretty powerful!

Aside: Reflections and projections

If you want to reflect and project across any plane, all you need to do is find an orthonormal basis that contains its orthogonal vector. Then, you can use change of basis to effectively move the coordinates to that plane, do what you need to do (reflect, project), then switch back again. Example: reflecton

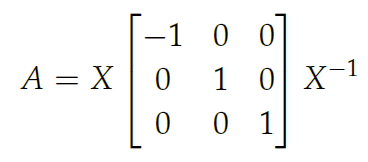
where $X$is an orthogonal matrix.