SVD (Single Value Decomposition)

SVD is just an extension of eigendecomposition where we have $A = U\Sigma V^T$, where U and V are square, orthogonal matrices. The null space of $V^T$ is the same as $A$ (which means that if $A$ is square but non-invertible, $V$ may still be non-square).

• The $\Sigma$ is diagonal and referred to as single values. It may not be a full diagonal

The full SVD:

So technically, the SVD is expressed as block matrix product

In this case, $V_2$ represents the null space of $A$, and $U_2$ represents the complement of the range of $A$. The SVD decomposes a matrix into the four fundamental subspaces.

The compressed SVD:

You can just rewrite the SVD as $A = U_1 S V_1$, and that is sufficient SVD. In this case, $U_1$ would be $d\times k$, $S \in k\times k$, and $V_1 \in k\times d$.

SVD on non-square matrices

The $U$ is in the output space, the $V$ is in the input space, and the $\Sigma$ is a rectangular projection matrix which removes a select number of dimensions before mapping it (invertibly) to the output. In other words, instead of $\Sigma$ being a scaling factor (in a full-rank square matrix), $\Sigma$ is a projection-scaler.

Good Visualization

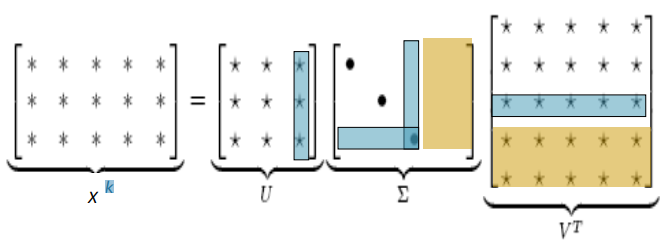
You basically have $U, V$ as transformation matrices, and $\Sigma$ as selecting the relevant rows of $V$ and scaling them. Note that depending on which way the rectangle goes, this $\Sigma$ will reject whole rows or whole columns. You can sort of understand this as doing the projection in a clean way. You’re rotating onto a good cutting surface with $V^T$, cutting with $\Sigma$, and then re-rotating with $U$.

Deeper theoretical look

Spectral theorem: for symmetric matrices, you can make an orthonormal eigenbasis such that $A = QDQ^{-1} = QDQ^T$ where $Q$ is the eigenbasis. Now, can we extend this idea to arbitrary $m\times n$ matrices?

Essentially, SVD extends the idea of an eigenvector to non-square spaces. To be brief, $A = U\Sigma V$ where $U$ is the eigenbasis of $AA^T$ and $V$ is the eigenbasis of $A^TA$.

Singular values

The singular values $\sigma_i$ of $A$ are $\sqrt{d_i}$. Now, $d_i$ are the eigenvalues of the symmetric matrix $A^TA$. Now, if $A$ were shaped $m\times n$, then there will be $\sigma_1, ...\sigma_n$ singular values. We list these in decreasing order.

More specifically, $A^TAv_i = d_iv_i$

Singular Value Theorem 🚀

If you have a $m\times n$ matrix $A$, if $v_1, ...v_n$ are orthonormal eigenbasis for $A^TA$, then

1. $Av_i$ are mutually orthogonal
   1. proof: $Av_i \cdot A v_j = (Av_i)^TAv_j = v_i^T(A^TAv_j) = v_i^Td_jv_j = d_j v_i\cdot v_j$. Now, we know that $v_i, v_j$ are mutually orthogonal, so we are done.

2. $||Av_i|| = \sigma_i$. Let $u_i = \frac{Av_i}{\sigma_i}$. You can imagine that $Av_i = \sigma_iu_i$, which means that $u_i$ is the "eigenvector" of $A$ in the $n$-space
   1. proof: we know from a previous result that $Av_i \cdot Av_i = d_j v_i \cdot v_i = d_i$. Because $\sigma_i = \sqrt{d}$, the proof is obvious.

3. More concretely: $v_1, ...v_n$ are eigenvectors of $A^TA$, and $u_1, ...u_m$ are eigenvectors of $AA^T$

4. $A = U\Sigma V^T$ where $U$ and $V$ are orthogonal matrices and $\Sigma$ is a diagonal $m\times n$ matrix.
   1. Proof: Consider $AV$, where $V$ is the column matrix of the orthonormal $n$-basis. We now that $Av_i = \sigma u_i$, so we can make a column matrix of $\sigma_n u_n$. This can be decomposed into a column matrix of $u_n$ and a diagonal of $\sigma$, with some sparseness (because recall that if $n > m$, there's got to be some $v_n$ that maps to $0$. Therefore, we get $AV = U\Sigma$, which mean sthat $A = U\Sigma V^T$ as desired.

Reduced SVD

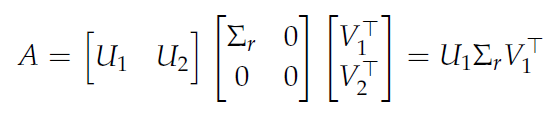
What does this mean in terms of the fundamental subspaces?

Well, the range of $U_1$ becomes the range of $A$.

The range of $U_2$ becomes the orthogonal complement to the range of $A$

The range of $V_1$ becomes the orthogonal complement to the null space of $A$

The range of $V_1$ becomes the null space of $A$

As such, the ranges of the four matrices cover the four fundamental subspaces of $A$!! By selecting $U_1 \Sigma V_1$, you are essentially piecing together the behavior of $A$.