Ranks

The rank is the dimension of the range of $A$

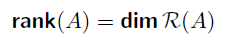
so it is dimension of the span of the columns (and rows, because of fact 1). Here are some facts: 1) the rank of $A$ is the same as the rank of $A^T$, and 2) $rank(A) + dim N(A) = n$ (the rank nullity theorem)

A full rank matrix has either independent columns (if it’s skinny), independent rows (if it’s fat), or non-singular (if it’s square, meaning that it’s invertible)

Rank Nullity Theorem

Let $A \in \mathbb{R}^{m\times n}$ (i.e. $T: R^n → R^m$)

The column rank is $R(A)$, and it's the maximum number of linear independent columns

the row rank is $R(A^T)$ and it's the maximum number of linearly independent rows.

This is very interesting. What does it implicate? it means that the following is true:

A $n\times n$ matrix is invertible if $rank(A) = n$

Linear Independence and Rank

The column rank of a matrix is the size of the largest subset of columns that form an linearly independent set. The row rank is the same, but for rows. It is provable that the column and the row ranks are the same value.

• if $A \in \mathbb{R}^{m\times n}$, $rank(A) \leq \min(m, n)$. As such, if $rank(A) = \min(m, n)$, it is said ot have a full rank

• $rank(A) = rank(A^T)$ (comes from how row and column ranks are the same)

• $rank(AB) \leq \min(rank(A), rank(B))$ (the idea is that matrices can't ever unsqueeze squeezed space.

• $rank(A + B) \leq rank(A) + rank(B)$

Rank, invertibility

The rank of the matrix is the dimension of the span of the columns of the matrix. It is also the dimension of the span of the rows. This is not a coincidence and there is a proof for this. Remember that dimension is the number of vector needed to define the subspace of the span; it doesn’t have to do with the number of elements in the column vectors. In SVD, the rank is the number of non-zero values on the diagonal.

A matrix is invertible if and only if it’s full rank, meaning that the vectors span the whole space.

When you compose matrices, you can never gain rank (duh). ⭐