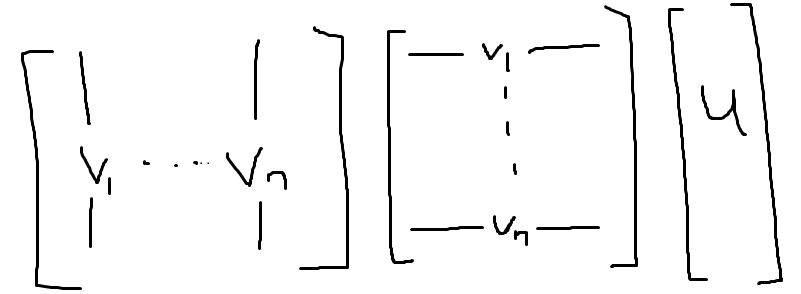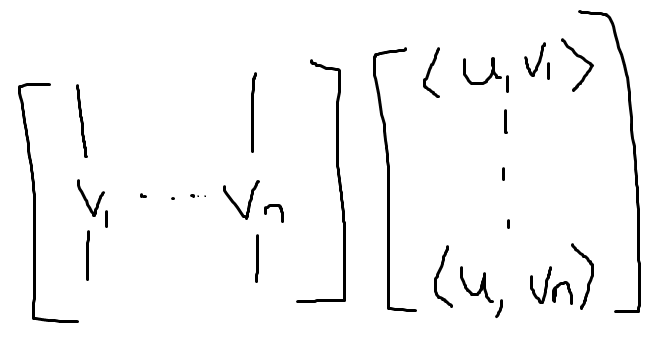The $\perp$ operator

$V^\perp$ is the set of all vectors $w$ such that $\langle w, v \rangle = 0$ for all $v \in V$. You can think of this as the annilator of a subspace in terms of our dual vocabulary.

Properties

Here are the properties (assume that $U$ is a subspace of $V$

1. if $U$ is a subspace, then $U^\perp$ is also a subspace

2. $0^\perp = V$

3. $V^\perp = 0$

4. $U \cap U^\perp = 0$

5. if $U \subset W$, then $W^\perp \subset U^\perp$

6. $V = U \oplus U^\perp$

7. $U^{\perp^\perp} = U$

8. $(V + W)^\perp = V^\perp \cap W^\perp$ (basically the "not" of two things together is the intersection of what they're not.

Projection operator

Inner products are understood as projections onto the target vector. Generally speaking, to project any vector $v$ onto $u$, we have

Projection onto Orthonormal Basis

A projection operator is very simple with an orthonormal basis: given an orthonormal basis $u_1, ...u_n$, we have

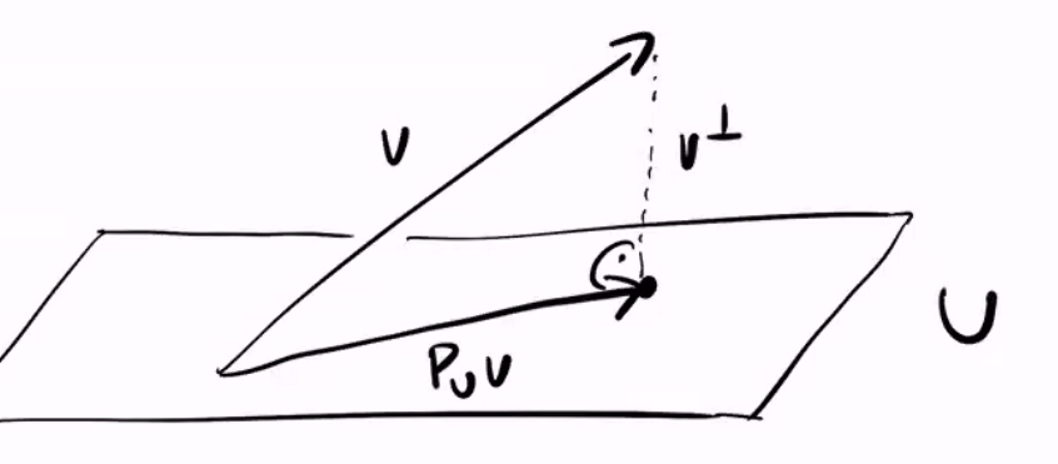
Projecting any vector onto any subspace is equivalent to projecting onto each individual component of its orthogonal basis and taking the vector sum (more on this later)

Properties

1. $P_U \in \mathcal{L}(V)$ (in other words, it is a linear map)

2. $P_U u = u$ (if $u\in U$)

3. $P_Uw = 0$ if $w \in U^\perp$

4. $range P_U = U$

5. $null P_U = U^\perp$

6. $v - P_U v \in U^\perp$ (intuitively, this is because $U \oplus U^\perp = V$; just rearrange this equation and you will see

7. $P_U^2 = P_u$ (makes sense)

8. $||P_U v|| \leq ||v||$ (also makes sense)

Projection as Contraction

You can prove that $|v - P_Uv|| \leq ||v - u||$ for all $u \in U$. Therefore, the projection operator vector is the closest vector to $v$ on $U$.

Projections as matrices

Suppose you had a set of orthonormal vectors $v_1, ...v_n$ that you wanted to project a vector $u$ onto. You would do the following:

As it turns out, if you let a $m \times n$ matrix $A$ be the matrix whose column is $v_1, ...v_n$, the projection operation above can be represented as

• Proof (visual)

  Why? Well, the explanation is purely visual

  

  You can think of the last two components as calculating the inner products:

  

• Refresher: Why $AA^T$ differs from $A^TA$

  Now, we know that $A^TA = I_k$, but because $A$ is not a square matrix, left inverses don't necessairly mean right inverses. You can imagine if $A$ were square, "projecting" a vector does nothing! this makes sense, because this square matrix would define the entire vector space, not the subspace!

Using projection

Linear regression

• you can perform linear regression by projecting $Y$ onto the subspace formed by $X, \{1\}$. By doing this, you will come up with an $m, b$ such that $||Y - mX - b\{1\}||$ is minimized. This is because projections minimize distance!

Closest distance between two parameterized lines

• if you have $a + tv$ and $b + t'w$, to minimize the distance, you're essentially minimizing the following:

And this is exactly the same as projecting the vector $a - b$ onto the span of $u, w$. And we know exactly how to do this!

• you can also find the closeset distance between two parameterized (and skew) lines by understanding that parallel planes pass through these lines, and you can find the distance between the parallel planes by adding components of the orthogonal vector (i.e. literally "shifting" the plane and then figuring out how much you shifted)

Adjoints

$\langle Tv, w\rangle = \langle v, T^*w\rangle$ . This is the property of an adjoint map

Now, this should be ringing alarm bells in your head, because this seems dangerously like dual maps, because it is!

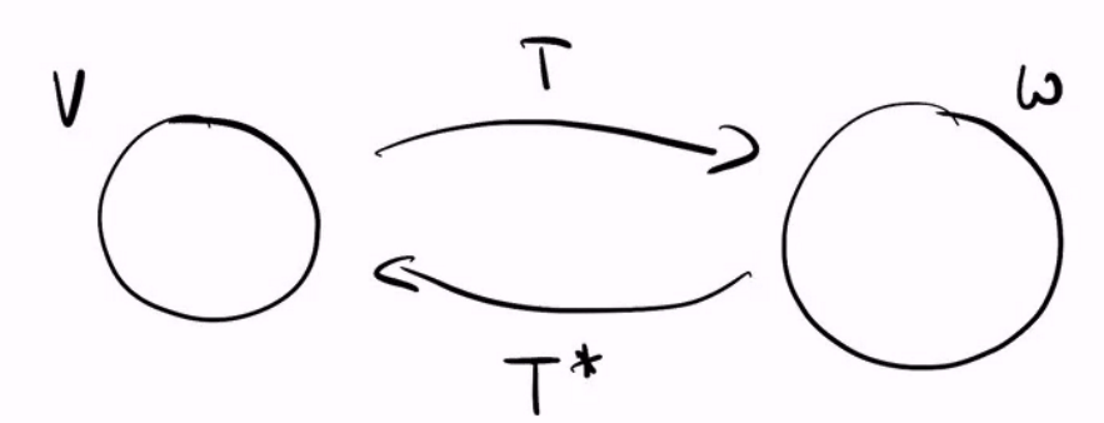
Matrix of the adjoint map

Without getting to much in depth, the adjoint matrix is the conjugate transpose of the normal matrix. Again, adjoint maps are literally just like the dual map. There are differences, but it’s not incredibly important.

Properties of the adjoint

1. $(S + T)^* = S^* + T^*$

2. $(\lambda T)^* = \lambda T^*$

3. $I^* = I$

4. $(ST)^* = T^*S^*$

5. $(T^*)^* = T$

Null and range

again, this is literally just like the dual space, so the same things hole

1. $null T^* = (range T)^\perp$ (relationshp between two of the four fundamental subspaces)

2. $range T^* = (null T)^\perp$ (the second relationshp between two of the four fundametnal subspaces)

Self-adjoint operator

$\langle Tv, w\rangle = \langle v, Tw\rangle$. This means that $T$ must be conjugate-symmetric!

Every eigenvalue of a self-adjoint operator is real, and all eigenvectors with distinct eigenvalues of a self-adjoint matrix is orthogonal. You can prove this by using the inner product definitions of a self-adjoint operator.

Normal operators

A normal operator is defined as one that commutes with its adjoint $TT^* = T^*T$. Obviously, every self-adjoint operator is normal.

In general, if $|Tv|| = ||T^* v||$ for all $v$, then $T$ is normal (and vice versa) You can show this by using the inner product definition of a norm.

• as a consequence, if $T$ is normal, then $T, T^*$ have the same eigenvectors with eigenvalues of conjugates of each other.