Orthonormal bases

Orthonormal bases have a simple two properties: $\langle u_i, u_j\rangle = \delta_{ij}$ and $||u|| = 1$.

The norm of an orthonormal list combination can be expressed as follows:

A matrix is orthogonal if its columns form an orthonormal basis. This can be formed through the spectral theorem from any symmetric matrix. $UU^T = U^TU = I$ for any orthogonal matrix $U$.

Projecting onto an orthonormal basis

this is actually really easy, because you can think about splitting a vector $v$ into a linear combination of an orthonormal basis, like $v = a_1 u_1 + ....a_n u_n$. To extract $a_k$, just take the dot product of that vector with $u_k$, and all the other vectors have dot products equal to zero!

Therefore:

• Refresher: Why $AA^T$ differs from $A^TA$

  Now, we know that $A^TA = I_k$, but because $A$ is not a square matrix, left inverses don't necessairly mean right inverses. You can imagine if $A$ were square, "projecting" a vector does nothing! this makes sense, because this square matrix would define the entire vector space, not the subspace!

Gram-Schmidt Procedure

Goal: Given a set of independent vectors, can you find an orthonormal basis?

Approach: find a vector that is orthogonal to all the previous results, and then normalize. Repeat until done. You can do this by “removing” the components of the current vector that contribute to parts of the existing vector set. This looks like

1. find orthogonal component to existing basis

   $w_j := v_j - \sum \langle v_j, u_i\rangle u_i$. This is just the difference between the current vector and the projection of this vector. Because $U + U^T = V$, you know that the difference of vectors is orthogonal

2. Normalize: $w:= \frac{1}{||w_j||}w_j$. This is so the orthonormal condition is met

• Algorithm

  

Generalized GS algorithm

If you have a list of dependent vectors, then you can do the exact same thing, but if you get a zero vector after projecting it onto the existing vectors, you just ignore that vector and don’t put down a basis vector for it.

However, you can take some nice conclusions from it. From the GS algorithm on a set of vectors $A$, you get $A = QR$.

1. You get an orthonormal basis, and the number of vectors is the rank of the original $A$

2. The $R$ is in upper staircase form, meaning that we may create vectors from the original $A$ without adding new terms, but never do we add more than one term per new vector in $A$

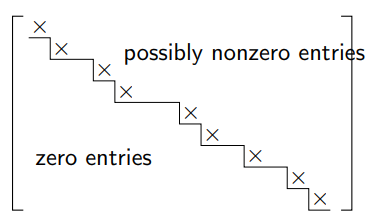
The staircase pattern also shows you which vectors in $A$ are dependent on the previous ones.

QR Decomposition

The QR decomposition is turning a matrix $A$ into an orthonormal matrix multiplied by an upper triangular matrix

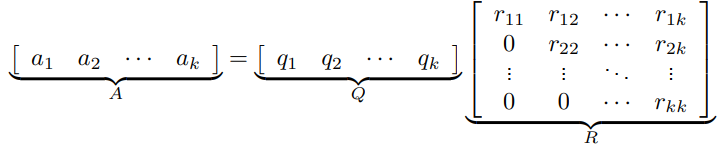
Fortunately, we already make this when we do the Gram-Schmitt algorithm! If we move the components around, we get

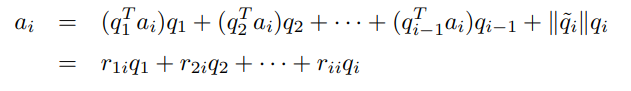
Full QR Factorization

If $A = Q_1 R_1$, the full QR factorization also include the other orthogonal vectors taht are outside of the span of $A$, which means that you start with

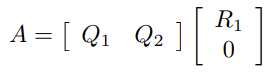
Then, you make a composite matrix with some matrix $\tilde A$ such that $[A \tilde A]$ is full rank. A foolproof method is to use the identity matrix. Then, after doing the GS, the extra vectors obtained from the columns $\tilde A$ go into $Q_2$.

Why do this? Well, $Q_1$ and $Q_2$ are complementary subspaces, known as the orthogonal complement. They are mutually orthogonal, and their subspace sums is the large vector space.

Schur's theorem ❓

Every matrix whose columns are linearly independent can be represented as an upper triangular matrix. Proof: take the linearly independent columns, find another basis by applying the GS algorithm, and then express the original matrix in terms of the GS basis. This is guarenteed to yield an upper traingular matrix! s

Orthogonal Matrix

A matrix is orthogonal if it is square and the columns are linearly independent. Orthogonal matrices are invertible and $A^T = A^{-1}$.