Vector-vector products

If we had a vector $x, y$, then $x^Ty$ i the inner product. On the other hand, $xy^T$ is the outer product, defined as follows

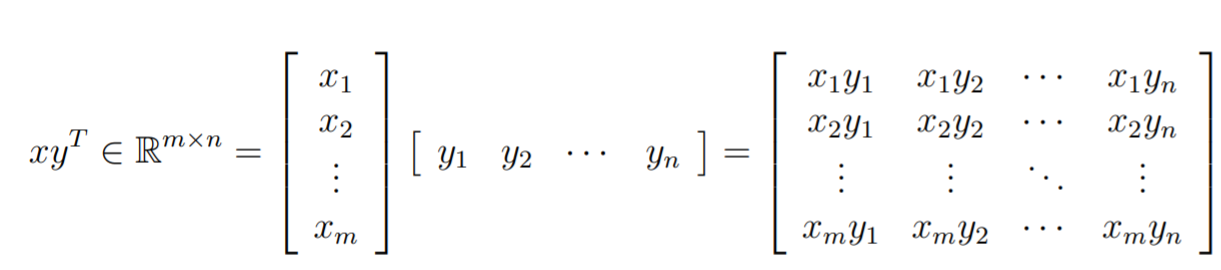
This can make your life easier if your matrix has a certain pattern to it.

Matrix-Vector Product

Matrix-vector product: row inner product interpretation

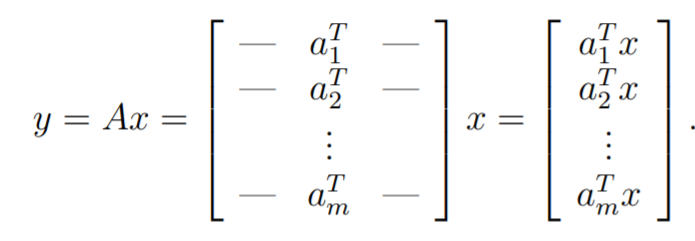
Matrix-vector product: mixture of column interpretation

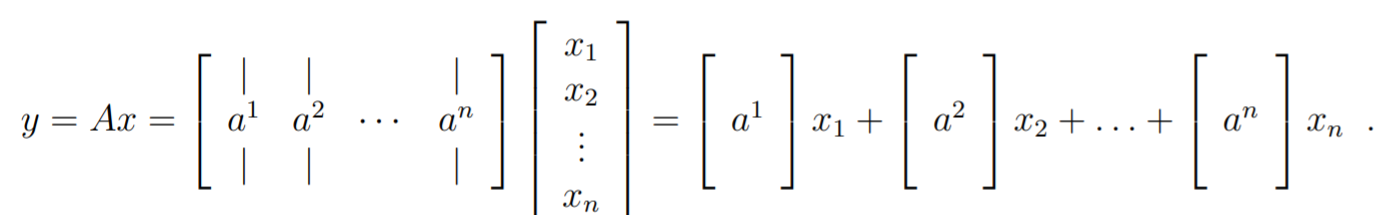
Intuitively, here is where we see the matrix as a definition of a new basis, where each column is a basis vector.

• Other interpretations

  Matrix-vector product: left hand side column interpretation

  You can also multiply on the left-hand side. This just means that you take the inner product with each of the columns. So in other words, it still is an inner product of sorts, but you do it to all the columns

  

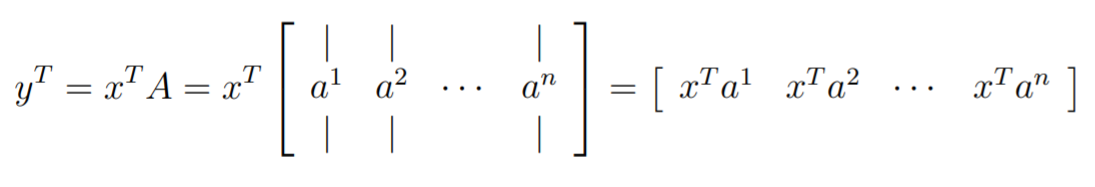
  Matrix-vector product: left hand side row interpretation

  You can think about the left hand product as also a linear combination of the rows.

  

  👉

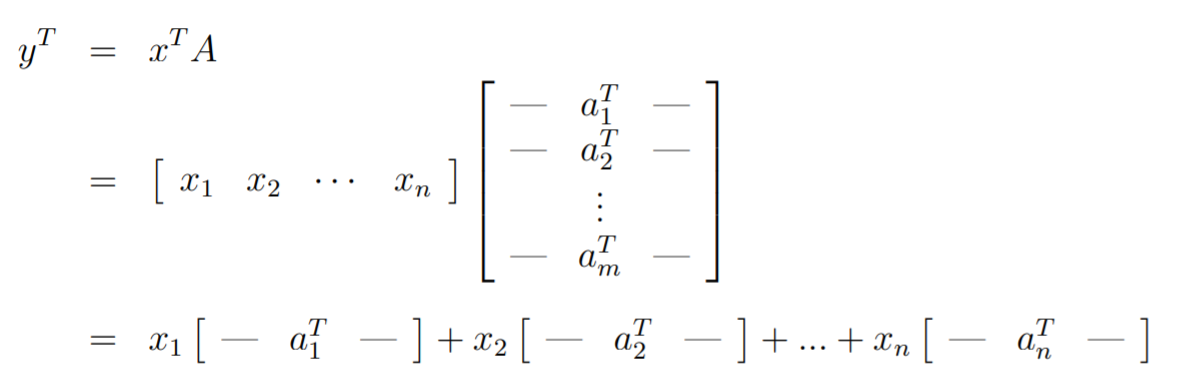  Note how the left hand side product is a dual to the right hand side product, with the two things switched in rows and columns. The most important thing to gain is this intuition of how matrix multiplication works!

Linear function interpretation

You can think of the matrix as a compact representation of a series of linear functions. If a matrix is $m \times m$, it can be "solved" with vector $x$ such that $Ax = b$. If it's $m \times n$ where $m > n$, then you have more "equations" then "variables" (more formally, you're mapping from lowdim to highdim). Therefore, you might not have a solution for $Ax = b$. Alternatively, if $m < n$, then you have more "variables" than "equations", so you will have infinite solutions.

Therefore, you can think of matrices as representations of functions, as well as functions itself!

Matrix-Matrix Product

The inner product interpretation

Every element at $i, j$ is just the dot product of the ith row with the jth column

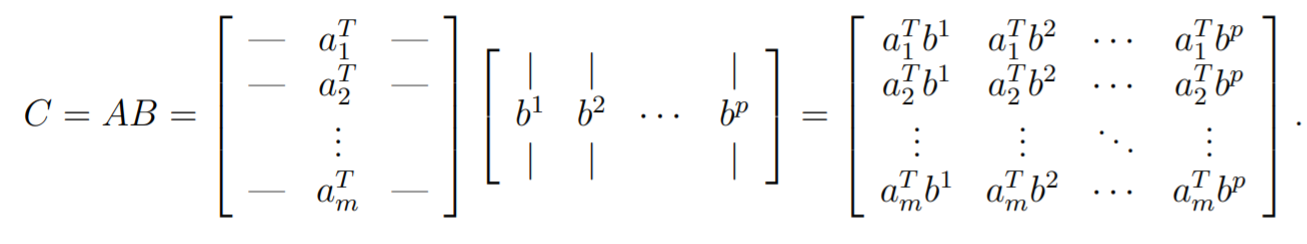
The Outer product interpretation

You can also think of the whole matrix product as a summation of outer products.

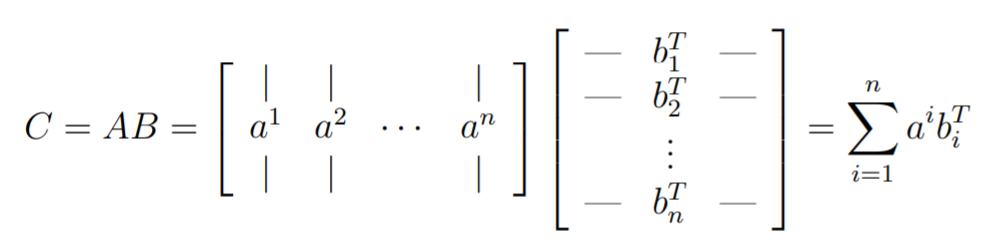
Column and Row Interpretations

You can think of the second matrix as a bunch of vectors (which it is), and it yields the following result

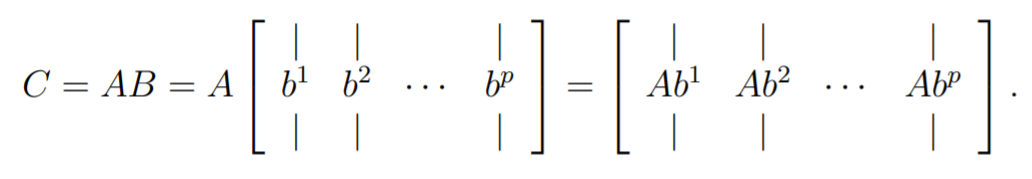
You can also think of the first matrix as a bunch of rows, which allows you to writ it like this

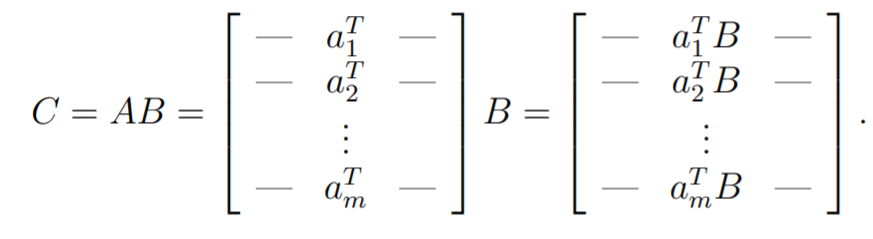
The geometric tie-in

A matrix is a function that maps from one set of basis vector to another set. To be more precise, $Au_1 = \sum A_{j, 1}w_j$. therefore, a matrix-vector product is a transformation of a vector. This is expressed as a linear combination of transformations of basis vectors, due to the linearity property of linear maps.

A matrix-matrix product is just a transformation of a set of basis vectors, which has already been transformed once by one matrix. It's akin to function composition.

The path interpretations

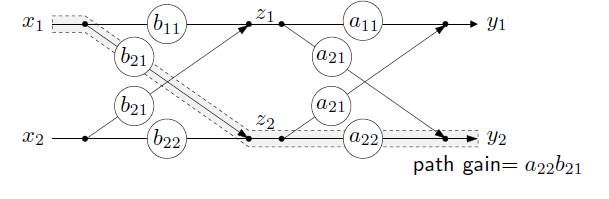
You can imagine an input $x$ and an output $y$, and we compose the two functions $A, B$. There are multiple paths from each element input to each element output, and the matrix multiplication is just summing up all the paths (one path above is highlighted)