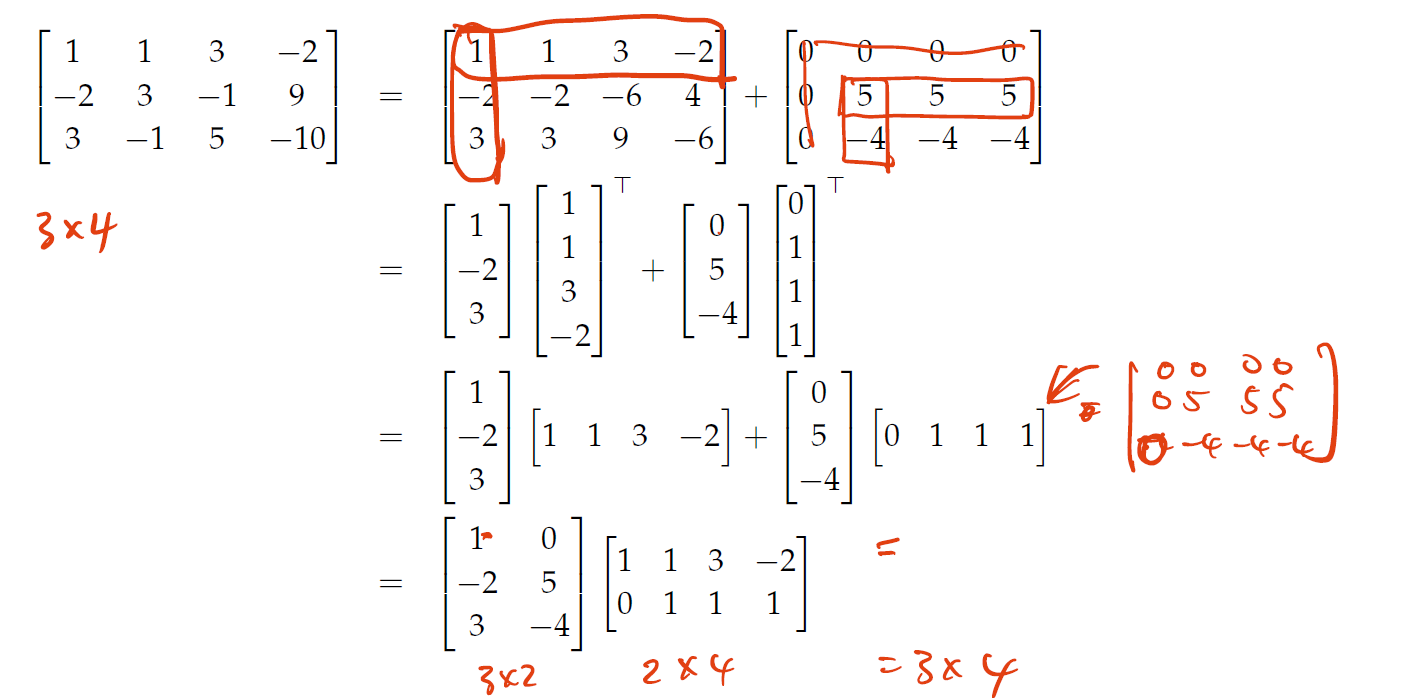
LU Factorization algorithm

Create $A_1$ that has the same first row and column as $A$, and the rest are filled by a multiplication table (i.e. row element times column element fills that element).

Create $B_1 = A - A_1$

Create $A_2$ from $B_1$ such that it has the same second row and second column as $B_1$, and repeat the filling in, and later, the creation of $B_2$

Keep on repeating until you get a zero matrix for $B_2$

We get $A = LU$, where the "L" is just the rows you created and the "U" is just the columns you created

• Example

  

CR Factorization

Every $m \times n$ matrix $A$ can be expressed as $A = CR$ where $C$ is $m\times r$ linearly independent columns and $R$ has $r\times n$ linearly independent rows

The construction is actually very easy. Think about the matrix multiplication as the column interpretation, and it will be pretty obvious what you have to do.

• Example

  

We call $R$ the reduced row echelon form of $A$. It is upper-triangular

Neat facts about the CR algorithm

• rows of R are LI, and the columns of C are LI

• the column span of $A$ is the same as the column span of $C$, and the row span of $R$ is the same as the row span of $A$. Take this at face value for now, we might come back to this later