The motivation

Previously, we used SVD to generalize eigenbases for non-square matrices. Now, we want to look at something different. If we had a square, defective (non-diagonalizable) matrix, can we make it as diagonal as possible?

Defining "as diagonal as possible"

To do this, we will show that we can express any matrix $A = X J X^{-1}$ where $X$ is a generalized eigenbasis for $A$ and where $J$ is in jordan Normal Form:

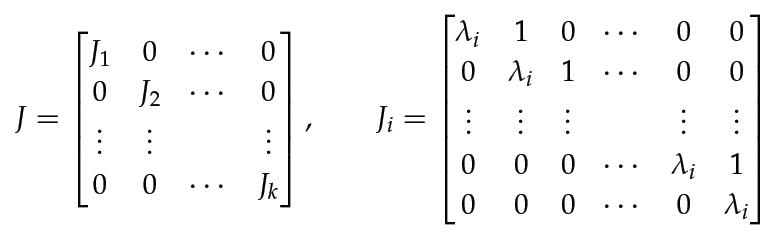
Generalized Eigenvectors

Increasing null spaces

Intuitively, the null spaces will grow. $\{0\} = null(T^0) \subseteq null((T^1) \subseteq null T^2 ...$ It makes sense because anything crushed to zero stays at zero, and elements in the range of $T^k$ may be in the null space of $T$

Interestingly, if there is some $m$ such that $null T^m = null T^{m+1}$, then all the null spaces from $m$ onward has the same size. You can prove this pretty easily by trying to show that $null T^{m+k+1} \subseteq null T^{m+k}$ (the other way around is by definition).

And intuitively, null spaces stop growing. More precisely, when the exponent is equal to $\dim V$, we are guarenteed to stop growing.

Generalized eigenvectors

In normal eigenvectors, $T - \lambda I$ sends eigenvectors to zero. generalized eigenvectors are such that there exists some $j$ such that for a generalized eigenvector $v$, $(T - \lambda I)^j v = 0$. We denote this generalized eigenspace as $G(\lambda, T)$.

Of course, the normal eigenvectors are contained within the notion of generalized eigenvectors

We can define $G(\lambda, T) = null(T - \lambda I)^{\dim V}$.

• forward direction: if $v \in null(T - \lambda I)^j$, then because null spaces keep growing, it certainly is in the exponent $\dim V$.

• Backward direction: by the definition of $G$, we can set $j = \dim V$, so anything in the null space of $(T - \lambda I)^{\dim V}$ become part of $G$.

Nilpotent Operators

A nilpotent operator (we've gone through this before) if some power of it equals zero.

If $N$ is nilpotent, then $N^{\dim V} = 0$. This is because null spaces stop growing at the $\dim V$ exponent, and nilpotent is defined to become zero at one point. As such, it must become zero before then.

Nilpotent operators have a basis such that the matrix is strictly upper-triangular, meaning that the diagonals are zero.

Jordan Form

A jordan chain of length $k$ is a sequence of non-zero vectors $v_1, ...v_k$ such that $(A - \lambda I)v_1 = 0$ and $(A - \lambda I)v_i = v_{i-1}$.

If $A$ has at most $k$ linearly independent eigenvectors, a Jordan basis for $A$ is just the union of $k$ Jordan chains, each Jordan chain coming from a $k$ right eigenvector. You can imagine these eigenvectors being the base case, and the chain expanding from that.

The number of Jordan chains is the geometric multiplicity of $A$.

Finding Jordan Chains

To do so, you start with the eigenvectors $u_1,... u_k$ of $A$, and then you set $Ax = u_1$ and solve for $x$. And you keep on doing this until you have no more solutions. Then, you move onto $u_2$ and continue.

Connecting back to the Jordan block

Each $J_i - \lambda_i I$ is a nilpotent operator. To be precise, it has a diagonal of zeros, and it maps $u_k$ to $u_{k-1}$ and $u_1$ to $0$. As such, you can imagine each "block" of the Jordan matrix as corresponding to one of the generalized eigenvectors $G(\lambda_i, J_i)$.

Each Jordan chain form the series of vectors that map down to the zero vector, so each Jordan chain corresponds to some $J_i$. Putting multiple Jordan chains together in a diagonal fashion produces the Jordan block matrix representation A

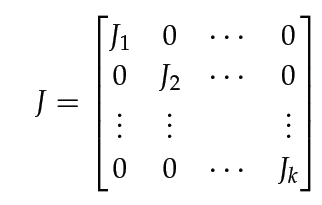
More about Jordan chains

Recall that we are only concerned with $J$ in some Jordan Basis that creates the Jordan Normal Form.

Jordan chains of length $n$ have jordan block matrices of $n\times n$. The most degenerate Jordan chain would be an eigenvector. As such, if $A$ is diagonalizable, then the Jordan Basis is just the eigenbasis and the normal form contains $n$ degenerate "block" matrices that are just individual numbers down the diagonal.

On the other side of things, you can have a Jordan chain be the length of the basis itself. As such, if $A$ is $m\times m$, then the Jordan "block" would also be $m\times m$.