Reisz representation theorem

Every linear functional can be represented as an inner product $\phi(v) = \langle v, u \rangle$. this is actually how we got to the idea of a linear functional, but formally, the linear functional comes before the inner product.

Inner products are actually derived from dual spaces.

Inner product spaces

Inner products can technically be anything, as long as it satisfies five properties. Dot product is one example.

1. positivity: $\langle v, v \rangle \geq 0$

2. definiteness: $\langle v, v \rangle = 0 → v = 0$

3. Additivity: $\langle u + v, w\rangle = \langle u, w\rangle + \langle v, w\rangle$
   1. works for the second position too

4. Homogenity: $\langle \lambda u, w \rangle = \lambda \langle u, w\rangle$
   1. $\langle u, \lambda w\rangle = \bar{\lambda}\langle u, w\rangle$ (note the bar)

5. Conjugate symmetry: $\langle u, v\rangle = \overline{\langle v, u \rangle}$ (\overline)

• Aside: Dot product with complex numbers

  • you want to satisfy $z \cdot z = ||z||^2$, and you know that $\lambda \bar{\lambda} = |\lambda|^2$, so it naturally follows that

  $$z\cdot w = \sum z_i \bar{w}_i$$

• Aside: Dot products with functions

  You can define $\langle f, g\rangle := \int_0^1 f(x)g(x)dx$, and it satisfies the properties above. This works with any sort of multiplier: $\langle f, g\rangle := \int_0^1 f(x)g(x)x^2dx$ is still an inner product definition. This is not just a toy example; this sort of inner product is used in fourier transforms!

  You can take the norm of a function! We can also use the idea that two functions are "orthogonal" to each other.

Derivable properties (and identities)

• $\langle a, b \rangle = a^Tb$.

• $\langle a + b, c\rangle = \langle a, c \rangle + \langle b, c \rangle$

• $\langle Ax, x \rangle = \langle \sqrt{A}x, \sqrt{A}x\rangle$
  • This is because $\langle Ax, x\rangle = x^TAx = x^T\sqrt{A}\sqrt{A}x$.

• $\sum \langle a, b_i\rangle = \langle a, \sum b_i \rangle$

• $||a-b||_2^2 = \langle a - b, a - b \rangle$.

Inner products of matrices

The corresponding norm of a matrix is the Frobenius Norm, which means that the inner product of matrices is naturally defined as

Norms

The norm of something is defined as $||v|| = \sqrt{\langle v, v \rangle}$. Two items $u, v$ are orthogonal if $\langle u, v\rangle = 0$. Therefore, norms are just a result of some inner product space. Norms satisfy these properties

1. non-negativity $f(x) \geq 0$

2. definiteness $f(x) = 0 \leftrightarrow x = 0$

3. homogenity $f(tx) = |t|f(x)$

4. triangle inequality $f(x + y) \leq f(x) + f(y)$

Holder norm (p-norm)

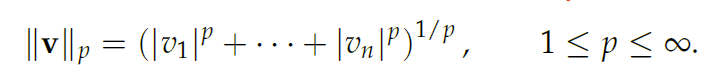
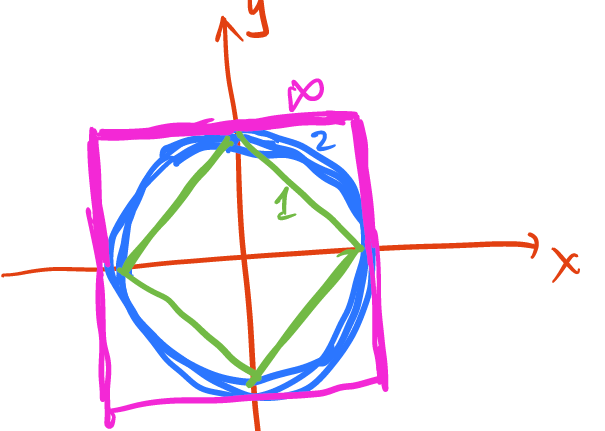
• If $p = 2$, you have your standard Euclidian norm

• If p = 1, then you just have the sum of the absolute values of the components, known as the Manhattan norm

• If $p = \infty$, then you have $||v||_\infty = \max^n_{i=1}|v_i|$ (known as the infinity norm, and it selects the largest value)

Frobenius Norm (matrix)

Frobenius norm is defined in terms of a frobenius inner product, i.e. $A^TA$. The frobenius norm is just $\sqrt{tr(A^TA)}$. By element, it is also $\sqrt{\sum_{i,j}A_{i,j}^2}$. This also means that $||A||_F = \langle A, A\rangle$

The norm satisfies all properties of the norm

• special property: if $U$ is a rigid transformation, then $tr(UA) = tr(A)$. Proof: $||UA||_F^2 = tr(AU^TUA) = tr(A^TA) = ||A||_F^2$.

• From this, we derive that the norm of a rank $k$ matrix can be reduced into the norm of a $k\times n$ matrix, or even a $k\times k$ matrix if you desire.

• Frobenius norm of a non-square matrix is still defined because of the $A^TA$.

• Like other norms, $||AB||_F \leq ||A||_F ||B||_F$.

Moral of the story here: if you want matrix-level properties, use the trace definition. If you want element-level properties, use the direct sum of squares definition

Operator Norm (matrix)

We define $||A||_{op}$ as the operator norm. The operator norm states that

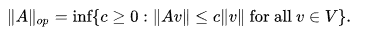
The operator norm is the same as the maximum eigenvalue of a matrix.

Matrix p-norms (matrix)

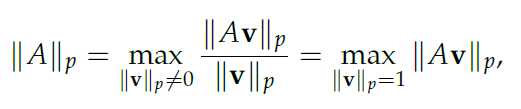
Essentially, find the vector that grows the longest with this transformation, using the p-norm (see previous section) as the metric

Spectral Norm of Matrix

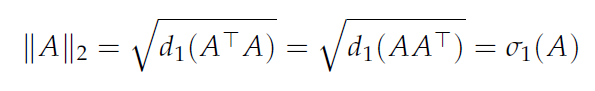
Derivable Norm / Inner Product Properties

Pythagorean theorem

$|| u + v||^2 = ||u||^2 + ||v||^2$ for any $u, v$ that are orthogonal. The proof is just an expansion of the norm into inner products and using inner product properties

Cauchy Schwarz

This has a ton of implications, because it generalizes to all inner products, including integrals. The proof involves decomposing $u$ into $\alpha v + v^\perp$ and then expanding out the right hand side in these new terms and applying pythagorean theorem.

Holder Inequality

The CS theorem is actually a specific form of the Holder Inequality, which applies as follows (where the subscript is the Holder norm)

Triangle inequality

$||u+v|| \leq ||u|| + ||v||$

You can prove this by using the inner product defintion and applying the Cauchy Schwarz inequality to get the inequality

Parallelogram Equality

The proof is just manipulating a lot of inner products around

Dual Norm

The dual norm to some norm is defined as

Intuitively, we take the boundary of the norm and see how to maximize the inner product.

• Dual of l2 is l2 (this should be obvious)

• Dual of l1 is infinity norm (intuitively: pick the coordinate that is the largest)

This dual norm property is a result of Holder’s inequality