Four fundamental spaces

Tags

The two common spaces

Nullspace

The nullspace is defined as

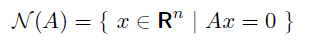
you can imagine it as the place where the matrix crushes the vector to zero. If we use the inner product interpretation, $N(A)$ is also the set of vectors that are orthogonal to every row of $A$ . It also means that you can add $x$ to anything and the $A$ will still output the same thing

Az = A(x + z)

The nullspace is itself a vector space. We will talk about the deeper meaning later.

We call $A$ as one-to-one if the only nullspace element is the zero vector. Equivalently, 1) the columns of $A$ are independent, 2) $A$ has a left inverse, and the determinant of the gram matrix 3 $A^TA$ is non-zero. We will establish these later

Range

The range is defined as

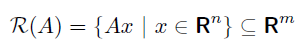
which is 1) the span of $A$ , and 2) the set of vectors $y$ such that $Ax = y$ has a solution.

If a matrix $A$ maps to the whole space, we say that 1) it has a right inverse, 2) the rows are indpendent, 3) it is one-to-one, 3) the determinant of $AA^T$ is non-zero. We will establish these later.

Four fundamental subspaces

In the input space, we have the null space $N(A)$ and the orthogonal to the null space $N(A)^\perp$ . These form the whole input space.

For the output space, we have the range $R(A)$ and the orthogonal to the range $R(A)^\perp$ .

All inputs map to the range (duh), although all inputs in the null space just map to zero. Here, we can make some assertions

It is necessary for invertible matrices to have an empty null space. If it is non-empty, then $0$ would have more than one solution, contradicting the invertible property. This is known as injectivity.

It is necessary for invertible matrices to have a full range. if the range is not full, then we can take something in the output space and not have something in the input space. This is known as surjectivity.

Invertible is satisfied with injective and surjective, meaning that only two of the four fundamental subspaces are non-empty.

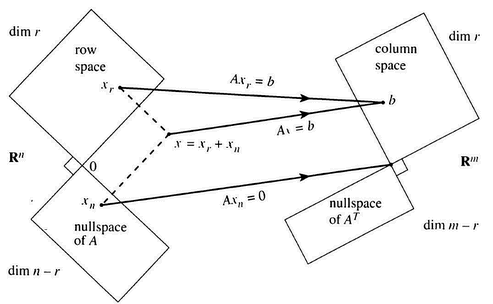
Inputs

We have the nullspace of $T$ , or $null(T)$ . If $v\in null(T)$ , then $Tv = 0$ . Another term for this is the kernel of the matrix. Another term that might come up is the right nullspace

We also have the rowspace of $T$ . Everything in the rowspace maps to everything in the column space of $T$ . Why is this the case? Well, this is complicated. The intution is that the rowspace maps toe the columnspace of the matrix. This intuition seems valid because you can think of the rows as "input" and the columns as "output". The formalism is better left until we discuss dual spaces. We will understand $A^T$ as the dual map of $A$ , and duals flip everything around.

These two subspaces are orthogonal to each other.

Outputs

We have the Column space of $T$ , which is just the range of the columns, and thus the range of the linear map.

We also have the nullspace of $A^T$ , which we call the left nullspace of $A$ . Again, this will make more sense when we get to dual maps, but essentially it's the dual of the right nullspace. You can't get to the left nullspace by applying $A$ .

These two subspaces are orthogonal to each other

Important properties

Row space is orthogonal to the null space (a). Column space is orthogonal to the null space of the tranaposed matrix (the dual matrix)

Other properties of fundamental subspaces

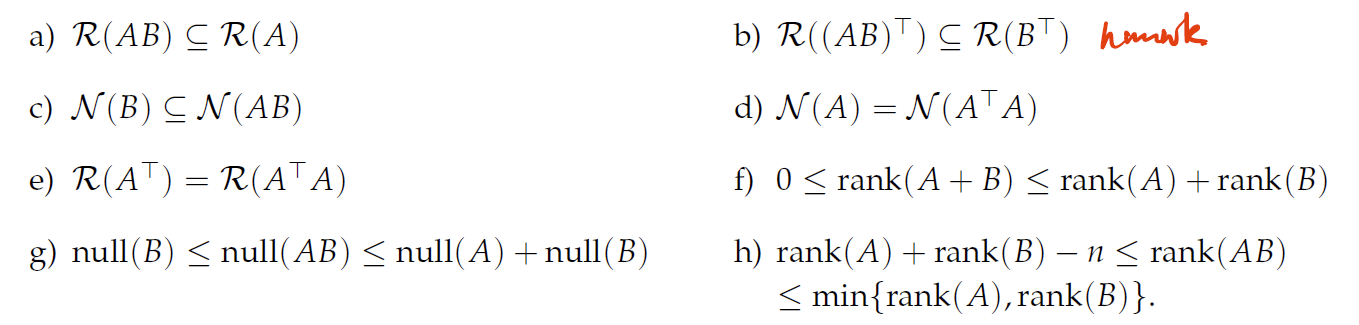
if $y \in R(AB)$ , then $y = ABx$ , which means that $y \in R(A)$ .

bit more tricky; probably uses some of the equivalences

if $x \in N(B)$ , then $Bx =0$ , so $ABx = 0$ , so the theorem holds

if $Ax = 0$ , then $A^TAx = 0$ , which is obvious. What about the other way around? $A^T(Ax) = 0$ , Therefore, $Ax$ is within the range of $A$ and also in the null of $A^T$ , but these are orthogonal complements of each other, so $Ax = 0$ .

follows from rank nullity