Eigendecomposition

Properties of Eigenvalues

• Always, if there is an eigenbasis, then the eigenvalues of $A^n$ is just $\lambda_i^n$. Proof: use diagonalization

• invariant to a rigid transformation (duh)

• Adding $\lambda I$ to a matrix will add $\lambda$ to all its eigenvalues

• If an eigenbasis exists for $A$, then $|Ax|\leq |\max(\lambda)x|$ for obvious reasons. But this is a nice property to know.

Gradient of eigenvalues

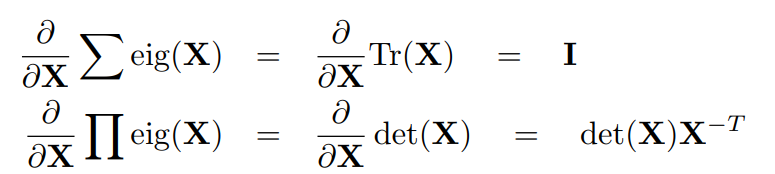
Sum and product of eigenvectors

The trace of a matrix is the sum of eigenvectors!

The determinant of a matrix is the product of eigenvectors!

Other Properties (cheat sheet)

1. The determinant of $A$ is the product of its eigenvalues

2. An eigenvector is defined as $Ax = \lambda x$, which means that $det(\lambda I - A) = 0$. We can use this to create a polynomial in $\lambda$ whose roots are the eigenvalues.

3. The trace of $A$ is the sum of its eigenvalues

4. The rank of $A$ is equal to the number of non-zero eigenvalues of $A$

5. Inverse matrices have the same eigenvectors as the original matrix but with eigenvalues as multiplicative inverses of each other.

6. $A, A^T$ have the same eigenvalues. This goes back to $det(A) = det(A^T)$

7. similar matrices have the same eigenvalues but not necessairly the same eigenspaces
   1. Proof: $A = XBX^{-1}$. This means that $det(A - \lambda I) = det(XBX^{-1} - \lambda I) = \det(X(B - \lambda I)X^{-1} = det(x)det(B - \lambda I) det(X^{-1} = det(B - \lambda I)$. Therefore, the characteristic polynomials are the same, and therefore the eigenvalue are the same

8. Cayley-Hamilton Theorem: $\pi_A(A) = 0$, for a diagonaliable matrix (i.e. when you plug the matrix into its characteristic polynomial it always yields a matrix of zeros. Interesting!
   1. proof: $A = XDX^{-1}$. Therefore $\pi_A(A) = X\pi_A(D)X^{-1}$. Now, $\pi_A(D) = 0$ because each element of $D$ is a root of the characterstic polynomial $\pi_A$. Neat!!

9. for a square matrix, eigenvectors that correspond to distinct eigenvalues are orthogonal (spectral theorem, more on this later)

10. right and left eigenvectors are linearly independent sets

11. eigenvectors corresponding to distinct eigenvalues are linearly independent

Creating eigenvalues

Invariant subspaces

An invariant subspace $U$ in $V$ is defined as the following: for all $u \in U$, we have that $Tu \in U$. Some examples of invariant spaces include the null space and the range of $T$, but also some other special vector spaces known as eigenvectors

Eigenvalues are defined under the following four equivalent conditions

1. $T - \lambda I$ is not injective

2. $T - \lambda I$ is not surjective

3. $T - \lambda I$ is not invertible

4. $\det(A - \lambda I) = 0$

It is this last point that we arrive upon the definition of the characteristic polynomial

Characteristic polynomial

$\pi_A(\lambda) = \det(A - \lambda I)$ is the `characteristic polynomial of $A$. The roots of the polynomial are the eignvalues.

• you can plug in matrices into polynomials if you want!

The eigenspace $V_\lambda$ is just $N(A - \lambda I_n)$, and it corresponds to all the vectors with eigenvalue $\lambda$

Multiplicity

The algebraic multiplicity of an eigenvalue is defined to be the dimension of the corresponding generalized eigenspace $G(\lambda, T)$. The geometric mulitiplicity is worried only with $E(\lambda, T)$.

• the algebraic multiplicity of an eigenvalue is just $\dim null(T - \lambda I)^{\dim V}$, because we have shown that the generalized eigenspace is equivalen the null space of $(T - \lambda I)^{\dim V}$

The sum of multiplicities is equal to $\dim V$

Mathematically, if $\pi_A(\lambda) = (\lambda - \lambda_1)^mf(\lambda)$, then $\lambda_1$ has algebraic multiplicity $m$

It is possible for geometric multiplicity to be strictly less then algebraic multiplicity, This is called being defective. In other words, there are some vectors that don't become eigenvectors until the $T - \lambda I$ is raised to a higher power. A defective matrix is not diagonalizable, while a non-defective matrix is diagonalizable, meaning that it has an eigenbasis

• in this case $A = XDX^{-1}$ where $X$ is your eigenbasis and $D$ is your diagonal.

Eigenspace

An eigenspace $E(\lambda, T)$ is just the span of all eigenvectors with eigenvalue $\lambda$. Alternatively, $E = null(T - \lambda I)$

The sum of eigenspaces is a direct sum, because different eigenvectors with different eigenvalues are linearly independent

Basis of eigenvectors

Sometimes you can have a basis of eigenvectors, which means that you have $u_1, ... u_n$ such that $Tu_1 = \lambda_i u_i$. The matrix of $T$ WRT this basis is just a diagonal, whose entries are just the eigenvalues

If such a basis exists, then you can find a mapping to this basis $X$ and represent the map as $X^{-1}DX$ or $XDX^{-1}$, depending on how you prefer to write it.

We will see some results involving this idea below

Another way of thinking about this

A square matrix has an eigenbasis if you can do $A = V D V^{-1}$ (or the other way around). As such, you can think of an eigenbasis as being able to stretch and shrink space in desired directions

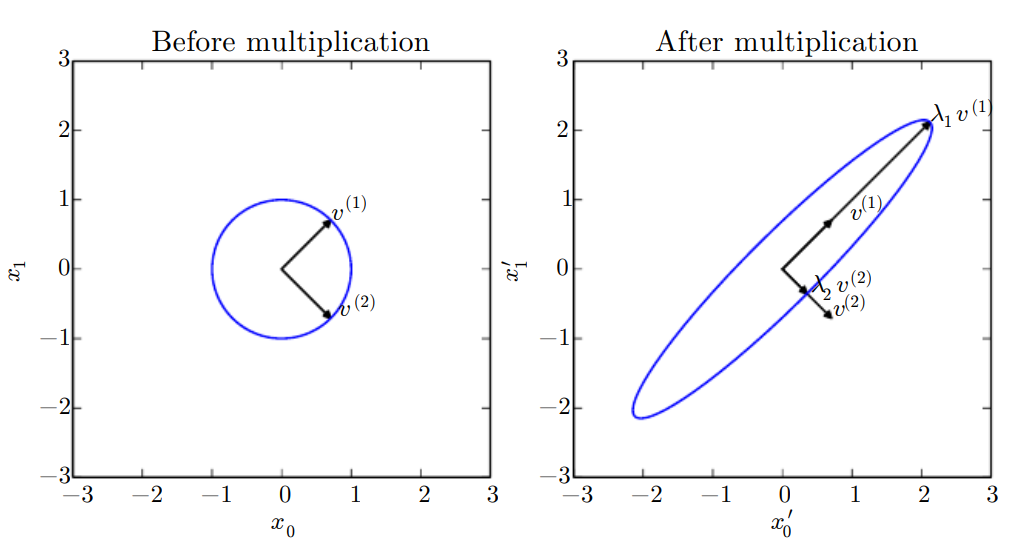
Diagonalization

We will build up the intuition why $A = UDU^T$. First, let's consider $AU$, where $U$ is a column matrix made up of the orthonormal eigenbasis $u_1, ...u_n$. This is as follows: (note that they use a slightly different symbol for the diagonal)

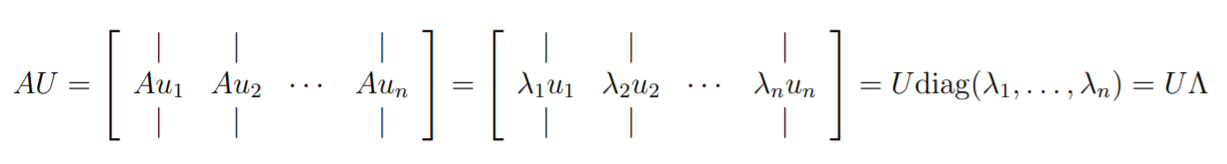
Now, note that $UU^T = I$, so we get the following:

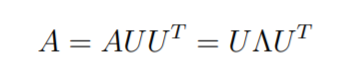
The importance of diagonalization

You can think of $U$ as a map that takes in vectors in an eigenbasis and pushes it over to the canonical basis. As such, $U^T$ takes the canonical and moves it to the eigenbasis. This is why it's $UDU^T$ and not the other way around.

Matrix-vector multiplication and matrix exponentials become very easy when dealing with an eigenbasis representation

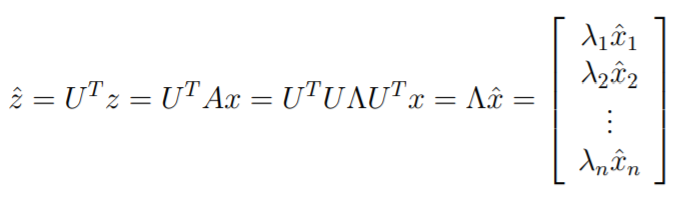
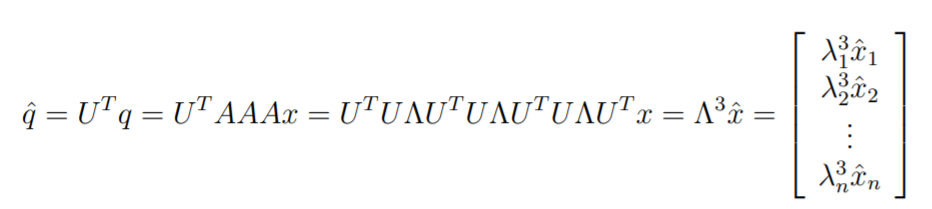
Other Formalities

Right and left eigenvector

A right eigenvector is such that $Ax = \lambda x$

A left eigenvector is such that $y^TA = \lambda y^T$ .

We will care more about right eigenvectors mostly.

Duality

The tranpose of a right eigenvector is a left eigenvector of $A^T$, and the tranpose of a right eigenvector of $A^T$ is a left eigenvector of $A$. You can prove this by tranposing the equation $Ax = \lambda x$

• you can also use this trick to find left eighvectors for $A$ easily using the characterstic polynomial of $A^T$

Properties

Quadratic form decomposition

If you have $x^TAx$, you can split it up into

Why? Well, the $U^Tx$ is the projection operation, which is equivlaent to inner product for unitary vector. Sigma scales, and associative property means that we can do $(x^TU)\Sigma (U^Tx)$.

Davis Kahan Theorem

If $A, B$ are $d\times d$ symmetric matrices and $||A - B||_F \leq \epsilon$, then

where $\lambda(A)$ represents an eigenvalue of $A$, and $v(A)$ represents an eigenvector of $A$.