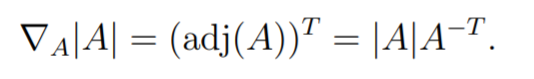Important Properties

Determinant is how the volume of the transformation changes

• determinant is just the product of eigenvalues (provable from the characteristic polynomial

• determinant is multilinear, so if you scale one column / row the whole determinant scales. Therefore, $\det(cA) = c^n\det(A)$ where $n$ is the dimension of $A$

• If diagonal or upper or lower-triangular, then the determinant is just the product of the diagonal of the mattrix

• $det(A^{-1}) = 1/det(A)$

• If the matrix is not full rank, then $det(A) = 0$ and conversely too

• Switching rows or columns of the matrix flips the sign of the determinant

• $det(A^T) = det(A)$ for real matrix

• $\det(A^n) = \det(A)^n$

• $det(AB) = det(A)det(B)$

• $det(A) = \prod \lambda_i$ where $\lambda_i$ is eigenvalue

Different interpretations

Recursive definition of the determinant

If we let $A_{\backslash i, \backslash j}$ be the matrix $A$ with the ith row and the jth column removed (known as the minor), then we have

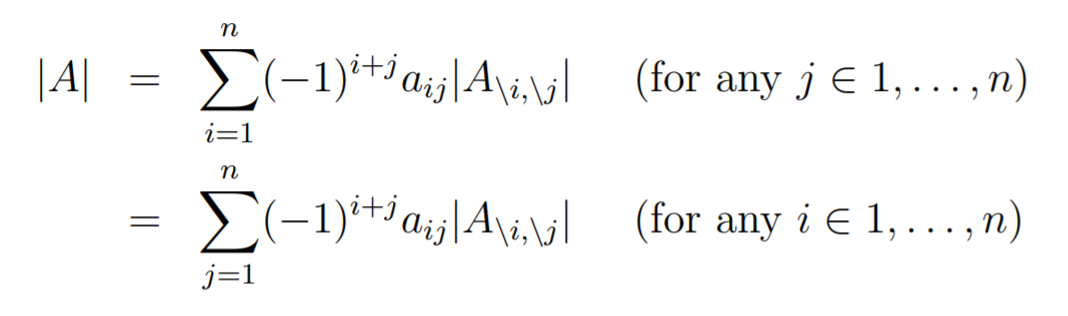
This fact is provable but it’s a little ugly so let’s just leave it be.

We can also define the adjoint recursively, as follows:

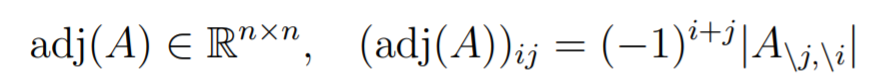
From this, we define the inverse

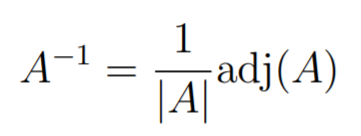
Permutation interpretation

A determinant is just the sum of all possible product permutations in a matrix. We define a permutation as the ways of scrambling $(1, 2, ... n)$. more precisesly, we generate a product for every permutation and add it up in alternating fashion to make the determinant

For more information, refer to the math 113 notes

Geometric interpretation

the determinant $\det (A)$ is the signed volume of a parallelepiped spanned by the column vectors of $A$

Multilinear function interpretation

A determinant is a multilinaer function (i.e. it takes in the columns of a matrix and it is linear WRT to each of the columns). It is also alternating. it is also the only such function that exists!

Properties

Multilinearity

Determinants are linear, and multilinear

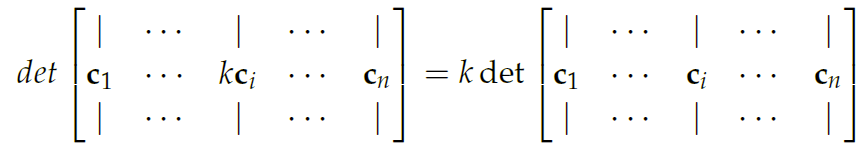
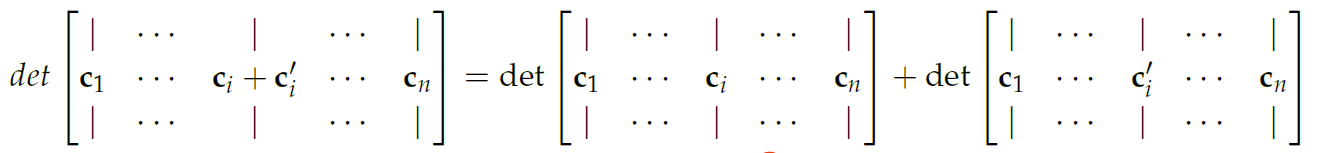
Alternating

determinants are alternating

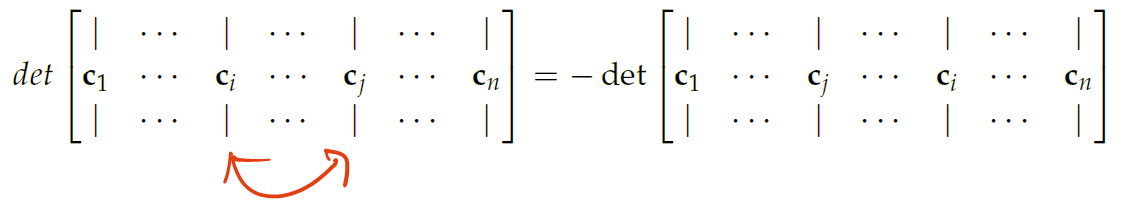
Transposes, products, and inverses

determinants are not affected by transposes (this hints at a deeper row-column duality)

• $\det(A^T) = \det(A)$

determinants are multiplicative:

• $\det(AB) = \det(A)\det(B)$

A matrix is invertible if and only if $\det(A) \neq 0$ and if $\det(A^{-1}) = \frac{1}{\det(A)}$

Determinants of a diagonal, or U or L matrix is just the product of the diagonals.

Determinants of a block diagonal matrix is the product of the determinant of each diagonal block matrix

Determinants of an orthogonal matrix is $\pm 1$, which hint at how these classes of matrices express rigid motions

Row and column operations

Taken together, we understand that adding any row to another row, or column to another column does not change the determinant of a matrix

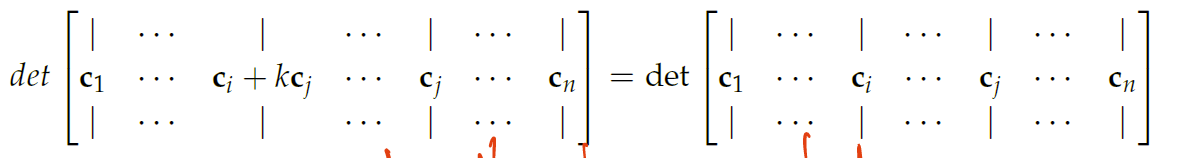
• this is because you can split it up, and the component with the duplicate column has a determinant of zero

Determinant properties: summed up

• multiplying a single row or column in $A$ by $t$ multiplies the determinant by $t$

• Exchanging a pair of rows or columns flips the sign of the determinant

• $|A| = |A^T|$

• $|AB| = |A||B|$

• If $A$ is singular, then $|A| = 0$

• $|A^{-1}| = \frac{1}{|A|}$

Gradient of the Determinant

You can just use the summation definition

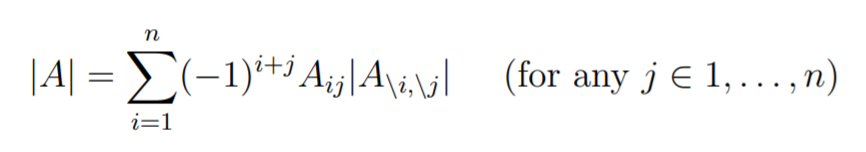
which means that

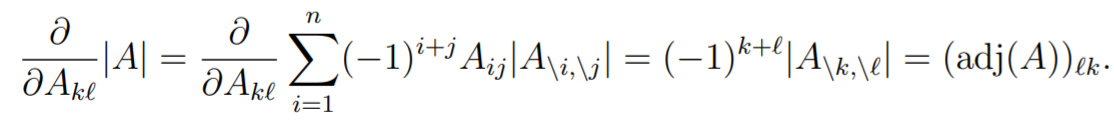
which means that