KL Divergence

KL divergence is a more involved form of cross-entropy.

This means that intuitively, DKL is the "loss of encoding efficiency" you get after switching from $P$ to $Q$ distributions. The more different the distributions are, the higher the DKL divergence.

DKL identities

We can prove that DKL is always non-negative. It requires a little trick of essentially multiplying by 1 and changing the expectation...

• Proof

  

  

We can prove that DKL is 0 IFF the two distributions are identical (meaning that their PDF's are the same)

• Proof

  

  

  

We can also prove that the DKL has a "chain rule", which is kinda obvious when you think about the log.

• Proof

  

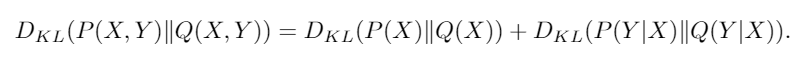
Observations about DKL

This section is purely supposed to be an intuition-based section that discusses what DKL actually does. For a more rigorous treatment, see my 228 notes.

For instructional purposes, say that we are fitting $q$ over distribution $p$ by minimizing $D_{KL}(Q || P)$ ( more on this in 228)

Maximizing the entropy

The first component is $\sum q \log q$, which is the negative entropy. By minimizing DKL, you are pushing $q$ to be as ehtropic as possible

Maximizing Log likelihood

The second component is $-\sum q\log p$, which means that you are maximizing the expected log likelihood of $p$ over a sample of $q$.

Overall effect

This means that you find the mode of the distribution of $p$ and then you "fatten" the distribution out to fill as much of $p$ as possible.

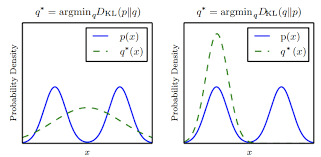
Asymmetry of DKL

$D_{KL}(q || p)$ cares about matching the distribution of $q$ to $p$. Fundamentally, it takes expectations across $Q$, so if you are dealing with a multi-modal distribution of $p$, a minimized $D_{KL}(q||p)$ WRT a single-mode $q$ will pick a single mode of $p$. However, if you tried minimizing $D_{KL}(p || q)$, then you are sampling from $p$. In this case, your best $q$ would be a large bump between the two modes of $p$.