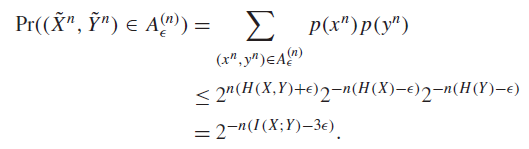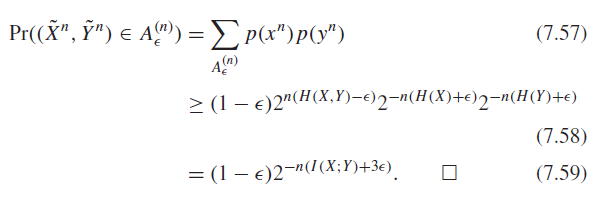Vocabulary

• We have $W → X^n → Y^n → \hat{W}$

• The $W$ is the message

• The $X^n$ is the input sequence. Individual $x^n$ are known as codeword. We sometimes use $X^n(W)$ to represent that there is an encoding process

Proof tips

• capacity is encoder agnostic, and with symmetrical channels, we know that the input sequence has to be uniform

Joint Typical Sets

So we have gotten us a nice property, a necessary condition of a noiseless encoder. However, we have made little progress on how we actually construct such a thing. In our discussion on compression, we essentially started with the concept of a typical set, and from that typical set came the primitive compression strategy. Let’s try a similar workup here.

We need the concept of a joint typical set because we have a set of inputs $X$ and a set of outputs $Y$ to the coding channel.

The Joint Typical Set Definition 🐧

A sequence $x^n, y^n$ is jointly typical if three conditions are met

1. $X$ is typical

2. $Y$ is typical

3. The equation below

• We need the first two conditions because otherwise, we can just have some very large number times some small number to yield a product within that bound. If $x^n, y^n$is typical, we automatically constrain what $p(y^n | x^n)$ is.

• Furthermore, even if X, Y|X is typical, you can perturb things enough such that the marginalized Y is not typical. So that’s why you need the additional Y constraint.

We arrived at this notion of bounding $p(y^n|x^n)$. This has a special meaning: let’s formalize this idea of conditional typical set:

This means that every output $y^n$ has a set of $x^n$ that is “most expected” to cause this $y^n$ output.

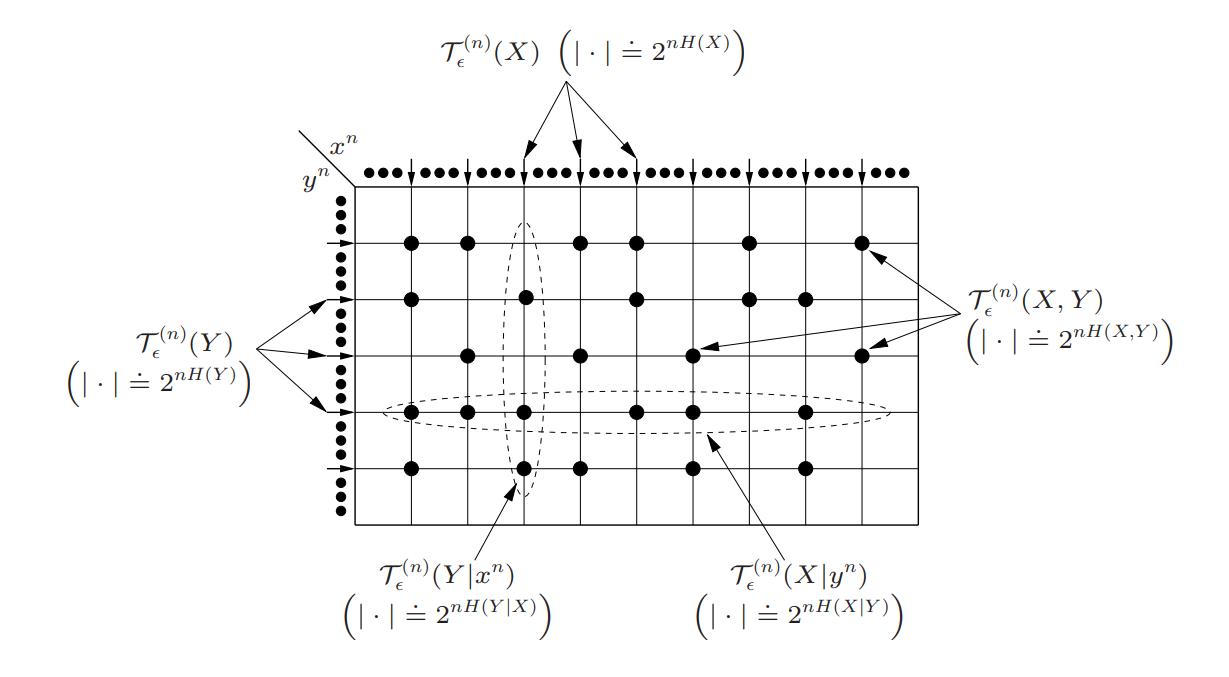
Understanding the relationship

• There is a large set of typical X and a large set of typical Y of sizes $2^{nH(X)}, 2^{nH(Y)}$.

• There is a set of X, Y whose joint probability is squeezed within $nH(X, Y)$.
  • there may be elements in this set that is not typical on marginal with X, Y (sometimes both)
  • You can imagine that at large numbers, these occurrences are rare.

• There are select tuples of $X, Y$ such that we form a joint typical set of size $2^{nH(X, Y)}$.
  • in this case, we impose the constraint that X, Y must be typical. In this case, the third point provides the constraint for the $p(y|x)$. The size of this true joint tyipcal set is less than $2^{nH(X, Y)}$

• For every X, there is a set of typical Y of size $2^{nH(Y|X)}$. These X’s don’t have to be typical themselves

• For every Y there is a set of typical X of size $2^{nH(X | Y)}$

Here is a good visualization.

Properties of Joint typical Set

1. $Pr(A) → 1$
   • Proof

     We know that all $X$, $Y$ converge to the entropy in probability, as well as $X, Y$ due to the law of large numbers and the AEP. Therefore, intuitively, the union of the set of things that don’t satisfy the jointly typical set will get smaller and smaller.

2. $|A| \leq 2^{n(H(X, Y) + \epsilon)}$
   • Proof

     Same as the proof for the singular typical set bound

3. $A| \geq (1-\epsilon)2^{n(H(X, Y) - \epsilon)}$
   • Proof

     

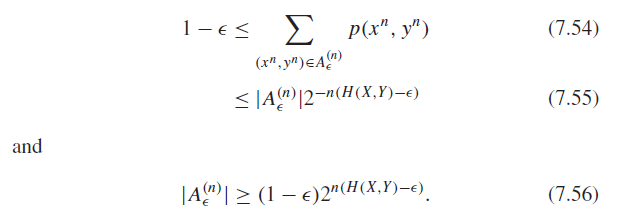
     The argument is actually very nuanced because there are X, Y that are not typical. We bypass this by using the AEP on the joint.

     As a back-of-the envelope calculation, at very large N, everything will be typical. The size of typical set of X is $2^{nH(X)}$, and the size of the conditional typical set is $2^{nH(Y|X)}$. If we assume that we can satisfy the Y typicality just because it’s far more likely to be tyipcal with Y at large N, then we can just multiply these together to get $2^{nH(X) + H(Y|X)} = 2^{n(H(X,Y))}$.

4. If we let $\tilde{X}\sim p(x^n)$ and $\tilde{Y} \sim p(y^n)$ (i.e. marginalize and pretend tnat X and Y are independent), then $Pr(\tilde{X}^n, \tilde{Y}^n \in A) \leq 2^{-n(I(X;Y)-3\epsilon)}$ and for large enough $n$, we have $Pr(\tilde{X}^n, \tilde{Y}^n \in A) \geq (1-\epsilon)2^{n(I(X;Y)+3\epsilon)}$
   • Proof

     

     This is true because 1) the inside probabilities are bounded because of the marginal restrictions on the typical set and 2) the size of the A is bounded.

     

     Similar reason as above.

We care about this last property because it basically says that the probability that a randomly chosen pair from the marginals is jointly typical is about $2^{-nI(X;Y)}$. A signal is unique if the pair is in the jointly typical set. There may be other confounding interpretations, but if it’s outside this typical set, then these get asymptotically smaller as $n$ gets large.

This indicates that there are $2^{n(I(X;Y)}$ distinguishable signals.

Channel Coding Theorem

The Setup 🐧

Let’s review some terms introduced in the previous section. We have $C$, the channel capacity. We have $R$, the rate measured in bits code per bit of channel. We have $m$, which is the number of bits in the message $W$ The diagram looks like this:

The number of bits in $W$ is just $nR$.

Sometimes, we denote the code as $X^n(W)$ which shows how this W is encoded through some sort of encoding (not compression; that’s done before W).

We assume that the channel is discrete and memoryless, which means that $p(y^m | x^m) = \prod p(y|x)$. This does not imply that all $X$ is independent. We do know that $W$ is IID uniform, but the coding algorithm may not choose to keep that IID uniform.

The Coding Theorem ⭐

We assert that if $R \leq C$, then the probability of error becomes arbitrarily small with a smart choice of code. It is not true for any code.

To prove this, we will first actually show that any randomly chosen code will yield a probability of error that gets arbitrarily small.

Why we care

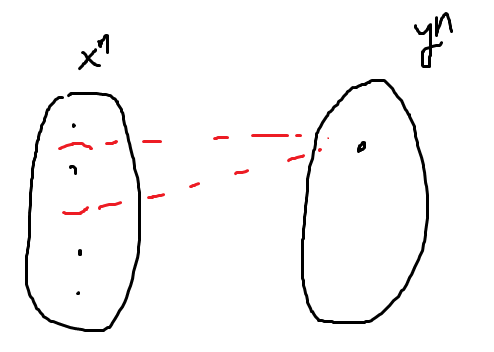
So essentially, we want to show that there exists some coding scheme (denoted as dots in the $X^n$ oval) where we can cleanly infer the input given an output $Y^n$. This is non-trivial. The red parenthetical is the jointly typical set given this $y^n$, and there are quite a few.

The proof

We start by making an important assumption: we only deal with typical sets of $X^n, Y^n$, because as $n$ gets large enough, all sequences become close to typical.

So let’s start with a randomly generated code. In other words, we start by generating a bunch of random $X^n$ and binding them to $W$. Why? Well, the $X^n$ would be uniform, and if we have a symmetric channel (our assumption), then we would be at capacity. Our limit of R is based on the fact that the P(x) hits capacity.

If the channel is symmetric, then the $X^n$ will be uniform and every $X^n$ is the typical set. This is the easiest to work with. If the channel is not symmetric, you will use the optimizing distribution $ber(p)$. This is slightly more complicated. For now, assume that every code we bind $X^n(W)$ will be in the typical set of $X^n$.

Now, the true $X^n(W)$ will be in the conditional typical set with high likelihood (by the AEP), so we don’t have to worry about that. Instead, we are concerned about some other $X^n(W’)$ being in the region of the conditional typical set of $Y^n$, which would be a problem. Why? Well, then there’s ambiguity in the decoding!

But here’s where the random code selection comes in clutch. From the AEP properties, we know that there is around $2^{nH(X | Y)}$ elements in the conditional, and $2^{n(H(X)}$ in the total typical of $X^n$. Therefore, the probability that another code lands in the conditional is just

So this is the probability of a single $X^n(W’)$ being in the conditional. What about all of the $W$? Well, we can easily set up a union bound

For context, remember that there are $2^{nR}$ different $W$’s. And the last inequality is where we use our original claim that $C > R$. The final equality comes from the assumption that the distribution of $X$ is chosen to meet the capacity.

From here, it becomes obvious. As $n→ \infty$, the $P(E)$ pinches down to 0. And the slower you send, the faster the error rate drops.

And finally, we need to make one final conclusion. As this error probability is averaged over the randomness over the channel AND random code (implicitly; all random codes have the same bound), we can use the law of averages to say that there must exist at least one code that does better than the average random code, so we are done.

Proof (more rigorous, different approach)

To actually prove this, we need to establish what an error is. An error can happen in two ways

1. The true code $X^n(W)$ is not in the typical set of $Y^n$

2. There are other imposter codes $X^n(W’)$ that are in the typical set of $Y^n$.

Now, let’s formalize this. Define event $E_i$ as the following:

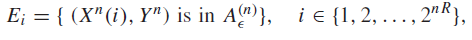
Error 1) happens when $E_i$ isn’t true at the correct $W$. Error 2) happens when at least one other $E_i$ is true at the incorrect $W’$. Using the symmetry of codes, we can just assume that we are coding $W = 1$. This yields the following

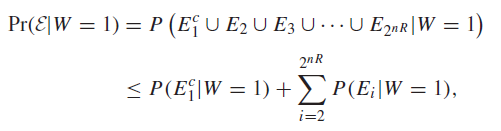
Now, we know from the AEP that the first term becomes smaller than $\epsilon$ for large enough $n$. From property #4 of the AEP, we know a bound on two sequences being in the typical set. This yields the following workup

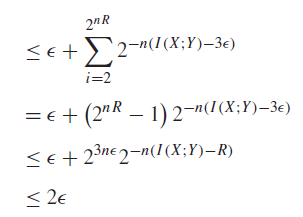
And so we have shown that the probability of error pinches down to zero!

The Bound on Communication

The communication limit 🚀

Here’s the a key theorem: if $R > C$, then $p_e$ is large, where $p_e$ is the error probability in transmission.

We will now prove this theorem by finding a lower bound on $p_e$. We see that in certain circumstances, the lower bound is zero. These are the times when it is possible to have an error-free code.

Proof: starting with Fano’s Inequality

Now, this is very lofty, because it seems like $p_e$ is very hard to quantity. However, let’s think for a second. The error probability sort of maps to the entropy of the decoding, given the input, right? Or, in other words, $H(W | Y^m)$. If we want to have an arbitrarily small probability of error, this conditional entropy should be near zero. Otherwise, it means that there is some uncertainty about the original message given the output of the channel.

Now indeed, as we remember from Fano’s inequality, we know that

where $m$ is just the size of the input, so $m =2^{nR}$. (to review, look at the notes on Fano’s inequality).

Moving towards the bound

Lets’ just consider $H(W | Y^n)$. We know that $I(W ; Y^n) = H(W) - H(W | Y^n)$, which means that

Now, because W is IID uniform, we know that $H(W) = nR$, which means that

Intuitively, this makes sense. The $W$ entropy adds noise, and the correlation between the input and the output can reduce some of that noise, but only to a certain point.

Now, because $W → X^n → Y^n$, we can use the data processing inequality to state that $I(W;Y^n) \leq I(X^n; Y^n)$. Therefore, we have

Let’s continue. We can factor the mutual information into $I(X^n ; Y^n) = H(Y^n) - H(Y^n | X^n)$. Now, the second term is very easy because of the discrete memoryless channel assumption. $H(Y^n | X^n) = \sum_i H(Y_i | X_i)$. The first term isn’t actually easy to compute, but we can bound it on independence. From this, we have $H(Y^n) \leq \sum_i H(Y_i)$.

Putting this together, we have

This last term depends on the channel properties as well as the distribution $p(x)$. However, we know a bound on this! It’s just $C$. So $I(X^n;Y^n) \leq nC$.

Putting this together, we have

Already, we are starting to see that if $R > C$, then the lower bound is non-zero, which is bad.

The final move, we just plug into Fano:

asymptotically. And this is exactly what we are looking for! If $R > C$, then the lower bound is non-zero, which means that the probability of error must be greater than this non-zero value.

Slight caveat on the bound

So this is based on the possiblity that $p^*(x)$ is reached. The more general result is

Because sometimes you might be artificially limited somehow to a class of $p(x)$ that doesn’t achieve optimality. So the lesson: your $R$ can’t exceed the CURRENT mutual information.

Simple case: zero-error codes

We can show the converse directly (without the contrapositive) if we know that the error probability is zero. The key here is that if $P_e = 0$, then necessairly, we have $H(W | Y^n) = 0$.

Then, we have

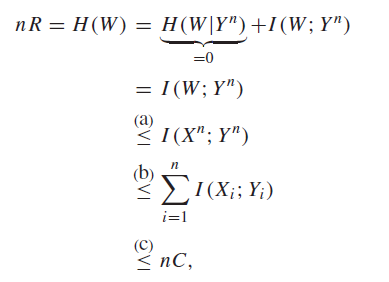
(a) is data processing inequality, (b) is independence bounding (see above), and (c) is predefined channel coding limit.

This is just the stripped down version of the proof above. In the proof above, we had to give a lower bound on $H(W| Y^n)$, and showed that this lower bound is only zero in certain cases.

Rates and Distributions

This is where I explain something a bit confusing.

So there’s this idea of an optimal distribution $p(x)$ that reaches $C = \max_{p(x)}I(X;Y)$. In binary symmetric channels, this is always uniform. But you shouldn’t assume that it’s uniform all the time. Because sometimes you might need to compromise, etc.

There’s this idea of an input distribution $u_1, …, u_n$, which we assume a priori that it is IID and uniform. So the message $W$ is uniform.

There’s this idea of an encoder $G(W)$ which takes $W$ and transforms it into $X^n$. This can and will entangle the individual bits, so $X^n$ is no longer IID. That doesn’t matter. As long as the individual marginals fit the $p^*(x)$, we are still at capacity.

So where does the rate come in? Well, you can always decide how much information you cram into $G$, i.e. how large your $W$ is. We don’t care how this $G$ is constructed just yet; we imagine that we can adjust it for different size $W$. The ratio of your $W$ size to the size of $X$ is your rate.

Now, if we assume that our $G$ can output $X^n$ distributed like $p^*(x)$, then the rate is restricted as $R \leq C$.

But what if that’s not the case? Well, then the rate limit changes. In the derivation of the Channel Coding theorem and the converse, we always bound $I(X; Y) \leq C$ and use $C$ to replace the $I(X;Y)$. Suppose that there is some tighter bound $C’$ due to some other constraint. It might be that your $G$ isn’t expressive enough, or you need to share a channel with something else, etc. In this case, you must replace the bound with this value.

Channel definition

You can define an arbitrary channel through the mutual information. You might have $I(X; Y_1, Y_2)$, which means that you send out one signal and you try to decode it by looking at two outputs. Every mutual information can yield a channel!