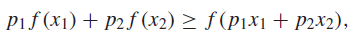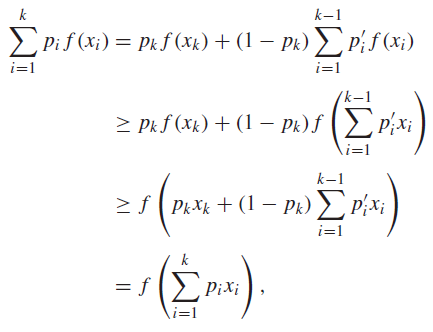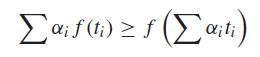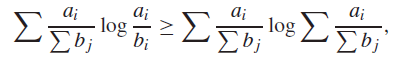Convexity

We define convexity (concave up) function as the following

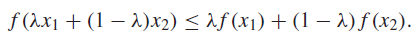
This should be intuitive, as the LHS is the curve segment, and the RHS is the secant line between two points.

When showing convexity, this is the definition we go to. Convexity is equivalent to having $f’’(x) \geq 0$, but that’s not the definition from first principles.

Jensen’s Inequality

Moving to RV’s

If $f$ is a convex function ,we assert this Jensen's inequality

The inequality flips if $f$ is concave (common use is $f = \log$)

• Proof (induction)

  We know from the basic inequality that this holds for two points.

  

  And we can extend this through induction. Suppose that it holds for $k-1$ points. Now, for a distribution with $k$ points, we have

  

  Using inductive hypothesis and the base case

As a side note, if $f$ is strictly convex, equality is achieved if and only $f$ if $X$ doesn’t change value.

Jensens with max, absolute value

So we know the following:

This is pretty easy to remember: boosting a value early on will yield a higher value down the line.

Strictly concave/convex

If a function is strictly concave / convex, then if $E[f(X)] = f(E[X])$, then we know that $X = E[X]$, meaning that $X$ is a constant value.

Log-Sum Inequality

The inequality

For non-negative numbers $a, b$, we have

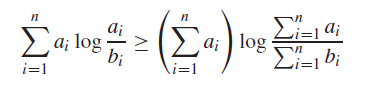
and equality when $a_i/b_i$ is constant. Essentially, this just allows us to push a summation into a log. It has a similar energy as Jensen’s inequality.

• Proof (Jensen)

  Let $f(t) = t \log t$, and let $\alpha_i = b_i / (\sum_j b_j)$. Because $\alpha_i$ is a distribution, we have by Jensens the following:

  

  If we let $t_i = a_i/b_i$, then we can fill in this inequality to get

  

  which is precisely the log-sum inequality

Gibbs Inequality

This one states that

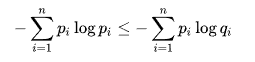
or in other words, your own entropy will be lower than using a different distribution. This has implications into optimal coding theory and some other topics. The proof is simple: when you combine the right hand and left hand side, you have KL divergence. We know that KL divergence is non-negative, which gives us the inequality.