Fano’s Inequality

Suppose that you knew a sample from $Y$ and you wanted to make an inference about $X$, a random variable correlated with $Y$. Can we say something about the fundamental limits of prediction?

The intuition

We can only estimate $X$ with perfect accuracy if $H(X | Y) = 0$, i.e. observing a $Y$ removes all entropy from $X$. So intuitively, the limits have to do with this conditional entropy.

The Theorem 🐧

Consider a markov chain $X → Y → \hat{X}$.

Let’s let $P_e = Pr(X \neq \hat{X})$. We claim that

which can be weakened (by letting H(Pe) = 1) into

• Proof (using an additional indicator RV and using some neat properties)

  Let $E$ be an indicator function, i.e. a bernoulli with probability $P_e$.

  

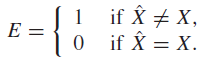
  And let’s consider the quantity $H(E, X | \hat{X})$. We can expand it two ways

  

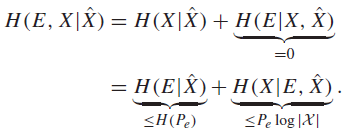
  The first zero is true because E is a function of the two X’s. The first inequality is true just due to entropy rules, and the second one is true using the following expansion

  

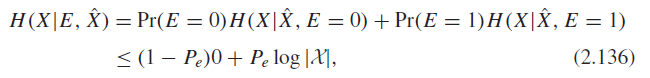
  The first component is zero because if E = 0, then X = X, and nothing is uncertain. Putting this together, we have

  

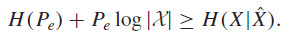
  And we can use the data processing inequality to derive that $H(X | \hat{X}) \geq H(X | Y)$, and so we are done.

Data Processing Inequality

A markov chain happens when we have $X →Y→Z$, where each variable is indepdent of all previous variables conditioned on the immediately previous one (markov assumption)

Remember that $X→Y→Z$ implies that $Z→Y→X$, as they are all active paths.

The inequality 🐧

The inequality states that if $X→Y→Z$, then $I(X;Y)\geq I(X;Z)$. In other words, you can’t gain information along the markov chain.

• Proof (MI chain rule)

  By the chain rule we get

  

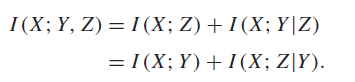
  and by the Markov assumption we know that $I(X;Z|Y) = 0$, and MI is non-negative, so $I(X;Z) \leq I(X;Y)$ as desired. It is also obvious why the equality condition holds here.

  Corollary 1: Equality happens if $I(X ; Y|Z) = 0$.

  Corollary 2: $I(X ; Y | Z) \leq I(X ; Y)$. This means that looking downstream will “spoil” the information upstream, which makes sense.

Now, due to the symmetry of the Markov chain, we also have $I(X ; Z) \leq I(Y ; Z)$, because we can just use the factor $Z → Y → X$, and the invariance of order in mutual information. In this case, the path $Z → Y$ is shorter than $Z → X$, so the mutual information is larger.