What is a Code?

A code is something that maps the domain of $X$ to a set of finite symbols. As the simplest code, you might give every element of the domain an index $i$ and use that as your code. We use $C(x)$ as the code, and $l(x)$ as the length of $C(x)$ (it’s a bit confusing, I know). We pick the symbols from an alphabet $\mathcal{D}$. Typically, we use $D = 2$ for binary.

We can extend a code by concatenating the code together. This creates a stream of information.

The expected length of a code is just $E_{x\sim X}[l(x)]$.

The rate of an encoder is the number of bits per sample. It is an average quantity, and it is bounded by entropy $H(X)$.

Getting a good code (what to look for)

1. A code must be bijective per character (i.e. no two inputs can map to the same output. This is called nonsingular.

2. A code must be decodable in sequence. This is known as uniquely decodable. Now, this may require you to look at the whole string and work your way backwards. Can we do better?

3. No codeword is a prefix af another. This is known as a prefix code. (or instantaneous code)

Code philosophy

A code and a compression is a way to take some distribution and turn it into something maximally entropic, which reduces the amount of bits needed to represent it.

Kraft Inequality

So instantaneous codes are really good, but they have a fundamental limit. In other words, you will create prefix collisions at a certain point. But at what point?

Kraft Inequality Definition 🐧

The Kraft inequality states that for an alphabet of size $D$ and codeword lengths $l$, the following must be true.

Conversely, this is also true: if there is a set of lengths that satisfy this inequality, there must exist an instantaneous code with these word lengths

Basically this is a necessary and sufficient condition for instantaneous codes.

• Proof (by tree)

  For this proof, let’s assume that $D = 2$. Now, a prefix code will have all codes as leaves of the tree. Think for a second why that’s the case.

  Next, consider the idea of a partition. You can extend any binary tree into a full tree by making more branches (see below). And you can imagine every node being a splitting point in the tree: the children that it has, and the children that it doesn’t have.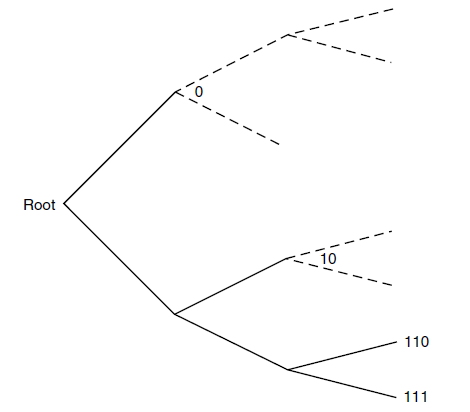

  

  Now, let $l_i$ be the length of every code segment. If you trace that code leaf down to $l_{max}$, i.e. continuing to branch, this leaf will have $D^{l_{max} - l_i}$ children at layer $l_{max}$. We know is that the sum of elements at layer $l_{max}$ is $D^{l_{max}}$. Therefore, we have the inequality

  

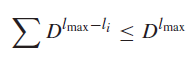
  which naturally becomes

  $$\sum_iD^{-l_i}\leq 1$$

  The inequality is possible because the prefix codes will never have a codeword that has children (otherwise the intervals will intersect).

  Now, why isn’t there an equality? Well, prefix codes come in different optimalities. It is true that optimal prefix codes will reach equality (every leaf node is used), but suboptimal prefix codes like $a = 0, b = 101$ will be less the right hand side.

• Proof of converse (by tree)

  Start with a full tree of height $l_{max}$. Then, take each $l_i$, find a trace in the tree, remove the descendants, and keep on doing this. The craft’s inequality ensures that you will always find another node that you can do this to.

Binary Kraft is Tight in Optimality 🚀

Essentially, if $D = 2$, then all optimal codes have

This is true by proof through a tree. Remember that $2^{-l_i}$ represents the proportion of the tree children that is “spawned” by this $l_i$. We make an inequality if we have a node that doesn’t have a filled leaf or a child node. But this means that the node is $→X→Y$, so we can “rotate” such that we have $X, Y$ share a parent. So there is no excuse to have suboptimality

Non-binary Kraft may not be tight in optimality

If $D > 2$, then our previous theorem doesn’t hold. It’s pretty simple. You can have some nodes without a full span of leaves (typically you want to put as many children as possible, but you may simply not fill all of the leaves). “rotations” aren’t a thing past $D > 2$.

Optimal Codes

Given that the Kraft Inequality is necessary and sufficient, we can use it as a constraint to find optimal but Instantaneous codes. In other words, we want to minimize

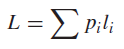
subject to

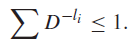
The tl;dr is that we want to find the shortest code given that we satisfy a certain property.

Implication of Constraint

So from the Craft’s inequality, we established that all optimal codes will have equality in the constraint ($\sum D^{-l_i} = 1$), which helps. We can use a Lagrange derivation (see below) or we can do something elegant that tells us a lot. Consider

Now, the cool part is that $D^{-l_i}$ is a distribution $q_i$, as it sums to 1. To get $l_i$ we compute $\log (1/q_i)$. Therefore, we have

As such we must conclude that $\sum_i p_i l_i \geq H(X)$, and this is a pretty significant point: it means that among the prefix codes, we can never reach below entropy in confusion.

Lagrange derivation (extra)

As you know, we can use the Lagrange multiplier to do constrained optimization

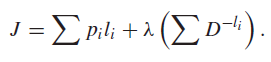
For every $l_i$ we get

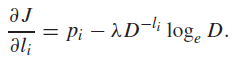
which gets us the solution

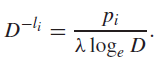
which essentially means that you should spend a longer code (smaller LHS) if the occurence is more rare ($p_i$ small), which makes sense.

After finding $\lambda$, we get that the optimal code length is just

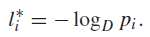
which is actually super elegant. Because if you plug it back into the expected length, we get back the entropy!

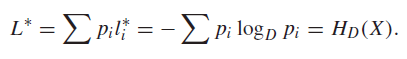
The optimal coding scheme ⭐

But this previous result also implicates something critical: the KL divergence means that if $p = q$, then the gap is tight. But recall the definition of $q$. In this case, $D^{-l_i} = p_i$, which means that $l_i = -\log p_i$. This is an interesting result: it means that the optimal coding scheme assigns a length to the code according to the probabilities in the distribution.

Integer Rounding

The problem is that we can’t guarentee that $-\log p_i$ is an integer. So we have to take the ceiling function (rounding down can violate the constraint). How much does that cost us? Well, here’s a general fact:

This should be pretty obvious why it’s the case. Therefore, the true length satisfies

Supervariables ⭐

So this one bit can be bad news, especially if $H(X)$ isn’t that large. But here’s the ultimate realization: it doesn’t matter how bit $H(X)$ is…the 1 stays the same! So what if we grouped a bunch of RV’;s $X_1,…,X_n$ together into a supervariable? Then, we have

which simplifies down to

So we can get pretty close as long as we start encoding multiple variables. But this isn’t a perfect solution. By putting chunks of variables together, we are increasing the complexity exponentially, which means that certain algorithms won’t be able to handle encoding in an efficient way (especially Huffman)

Wrong Codes (extra)

What if you used a coding scheme that is optimal for $q$ under a new distribtuion $p$? well, it turns out that you can bound it with

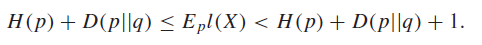
which is actually pretty cool, as it gives you a pretty tight interval.

• Proof (use of definitions)

  

Kraft Inequality for Uniquely Decodable Codes

So the Kraft was working with Instantaneous codes (baked into the tree proof), but as it turns out, any uniquely decodable codes will also satisfy Kraft.

• Proof (definitions)

  The problem is that we no longer have the tree at our disposal, as the codes may not follow that structure anymore. You have to start from first principles.

  The key is to raise the whole thing to the power of $k$, which leads to the following expression

  

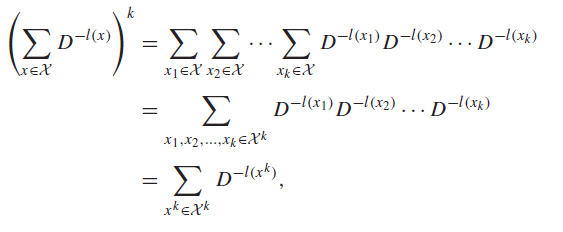
  why does this help? Well, now we’re working with sequences of length $k$, and we can change the index of summation from sequence index to code length

  

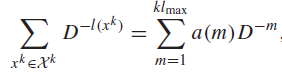
  where $a$ is the count variable. But here’s where we slide in the uniquely decodable thing: each code is unique by our setup, so there can’t be more than $D^m$ codes per length $m$, or else there will be intersection. So we have

  

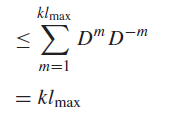
  and going back to the original summation, we have

  

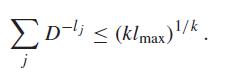
  for all $k$. So we take the limit of $k→\infty$, and we get

  

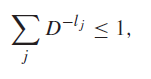
  as desired.