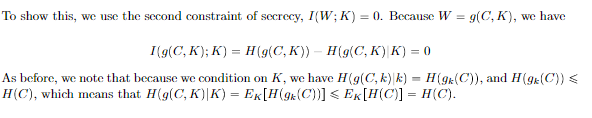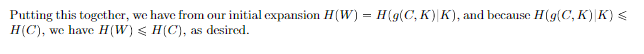Distributed Compression

Say that you had $X, Y$ correlated with entropies $H(X), H(Y)$. Say that you want to send both of them to a receiver. We can, of course, just use channels with rates $R_x = H(X), R_y = H(Y)$. But given that X, Y are correlated, can we do better?

So this is actually a hard problem because the encoders for X, Y don’t have access to each other.

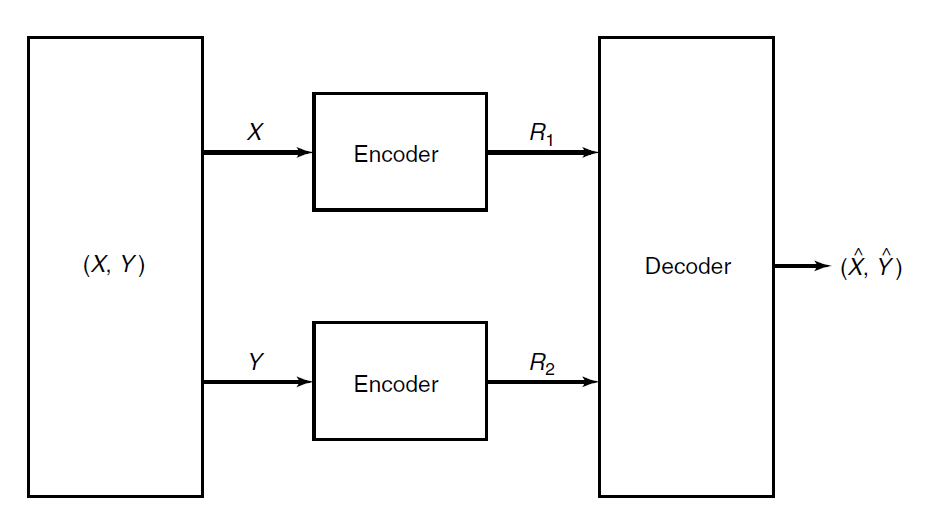
Toy motivation

Say the encoder and decoder had access to $Y$. Then, you can send $X$ at a rate $H(X | Y)$, which is more efficient.

However, this is a pipe dream because we don’t have real access to $Y$ during encoding. But now, we know that there is an interval $[H(X | Y), H(X)]$, and the optimal coding rate lies in there.

Slepian & Wolf (Distributed Compression)

In this setup, we assume that the decoder has access to the sent Y, and that this has no errors. We can essentially use a glorified hash function. We compress $X$ by using a hash function, and then we use a notion of joint typicality at the decoder to infer, among all the hash collisions, which $X$ is most likely.

The algorithm

Let’s assume that we have pure access to $Y$ at the decoder. This means that we need $R_Y \geq H(Y)$. If this is satisfied, then we do the following

1. Pick a hash function $\phi$ with $2^{nR}$ values, where we pick $R$ later

2. Hash $\phi(x^n)$ and deliver the bin index to the decoder

3. Using the decoder, look at the indexed bin and find the element that is in the typical set of $X | Y$ ( we assume access to this distribution). If we can find a unique result, return it. Else, return failure.
   1. Concretely, we look at the $2^{nH(X)}$ typical sets of $X$, and there are $2^{nH(X | Y)}$ bins, so every bin has $2^{nI(X ; Y)}$ typical sequences of $X$. This actually can form a grid where one axis is bin and the second axis is the bin index. The area is just $2^{n(H(X))}$. The grid is uniformly distributed because it’s a typical set.
   2. Without knowing the bin index, this is a really bad situation because you have $2^{nH(X | Y)}$ options from the typical set.
   3. Without knowing $Y$, this is a really bad situation because you have $2^{nI(X ; Y)}$ options.
   4. But what if you know both the bin index and Y? Well, here’s the interesting part. There are $2^{nH(X | Y)}$ options and there are $2^{nH(X | Y)}$ bins. So in expectation, there is only one option per bin. There is only one option that satisfies both $Y$ and the bin index. This is why decoding is possible!

• The formal proof

  We can show that the probability of error is arbitrarily small by using three possible errors and the union bound. 1) received $X, Y$ not jointly typical. 2) received X is a collision with another element in the typical set. 3) received Y is a collision with another element in the typical set.

  All of these are bounded. The first error is just AEP joint error. The second error we can calculate

  

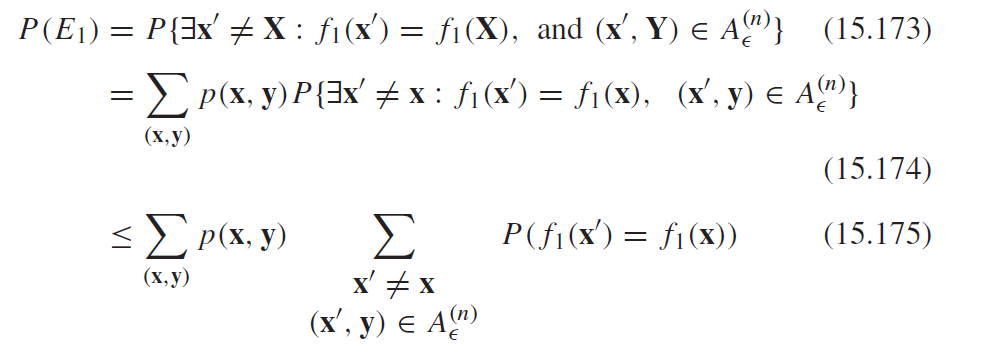
  Now, this probability is just uniform and just $1/2^{nR_1}$ because of the random hash. So we have

  

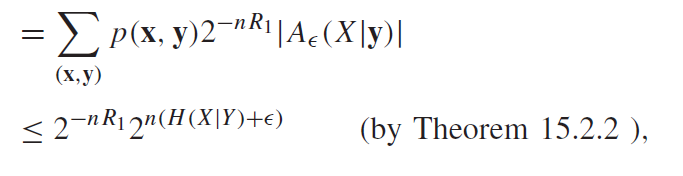
  And here, we see that as long as $R_1 > H(X | Y)$, the error goes to 0.

Picking $R$

So we can show that this algorithm works if $R > H(X | Y)$. There are $2^{nH(X | Y)}$ typical sequences per $Y$, Therefore, there should be $2^{nH(X | Y)}$ bins. This is very handwavy, and indeed you can’t do any strong guarentees. You essentially want all your hash collisions to be with non-typical sequences, but you can’t guarentee it.

How good can this algorithm get?

So we can actually establish three critical restrictions that tells us how good we can actually get.

• If the encoder for X were given Y, then it transmits with rate $R_1 \geq H(X | Y)$

• If the encoder for Y were given X, then it transmits with rate $R_2 \geq H(Y | X)$

• If the encoder worked with $X, Y$ jointly, then it transmits with a rate $R_1 + R_2 \geq H(X, Y)$

We know that the corner point is $H(Y | X) + H(X | Y) \leq H(Y | X) + H(X) = H(X, Y)$, which means that the third restriction is actually meaningful. At the end of the day you get the following rate region for this encoding approach:

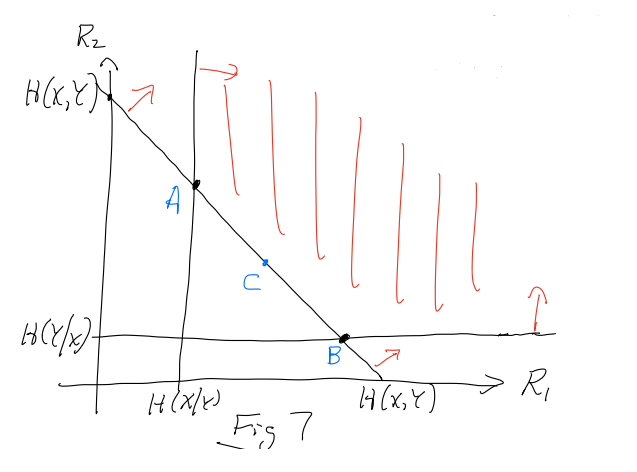
Now, it is possible to achieve point $A$ if we transmit $Y$ at full rate and $X$ at the restricted rate given the hash function. Now, recall that this isn’t the same as giving $Y$ directly to the X encoder. Rather, we showed that the hash function approach can yield the same rate lower bound!

It is possible to achieve point $B$ if we transmit X at full rate and Y at the restricted rate.

Now, we can achieve any point on the connecting line by just transmitting using the two strategies with varying probabilities. In other words, you might have two types of encoder structures created and during transmission, you flip a weighted coin.

Cybersecurity

In cybersecurity, you want to send $W → C → W$ where $C$ is assumed visible. Now you want to have $I(W; C) = 0$. How can this be done?

Well, you might have a secret key $k$ and the code comes from $C = f(W, k)$.

Coding theorem

Shannon stated that to have perfect secrecy, you need $H(k)\geq H(W)$. To achieve this, it’s actually quite trivial. Take $k$ as IID $Ber(0.5)$ and do XOR. If you xor any $k$ this way, you will get $C$ as also IID (because you randomly bit flip; it doesn’t matter where you come from). And the receiver just need to do XOR the $k$ again.

• Proof of the coding theorem

  

  Next, we want to show that $H(W) \leq H(C)$

  

  

Can we extract this $k$ without sending it?

Common Randomness

So in an ideal world, if we have some correlated $X^n, Y^n$, can we extract some meaningful random $k$ that is shared the two sides? Intuitively, we can. If there is correlation, there is shared randomness between $X, Y$, as measured by $I(X; Y)$, which we can try to extract.

So this sounds trivial at first: what if we just combined $X, Y$ and generated a random $k$? So that would work perfectly, but this would be a security risk. Remember that $k$ represents a security key and that Eve can look at any sort of communication. To produce this $k$, you would need to share $X, Y$ across this channel. So you can assume that Eve can construct $k$ too, which would make your code meaningless.

So here’s the revised problem statement:

1. You are given two correlated data streams $X^n, Y^n$. One is sent to Alice, and one is sent to Bob. Don’t worry about how these streams are created.

2. You can communicate some message $m$ across a public channel

3. You want to create a shared random key $k$ that both parties will share in common with high probability

4. You want the message $m$ to give away as little of $k$ as possible

The common randomness solution

So here’s the thought process: if we can get $X$ to Bob in a convoluted way and have Bob use his knowledge of $Y$ to decode $X$, then we can use the remaining randomness of $X$ as the shared key. Why? Well in this ideal situation, both Bob and Alice have copies of $X$. If they can systematically know what part of $X$ they reveal in the public channel, they can both peel back this known randomness to expose a secret core. They do this independently and require no communication.

All of this sounds fine, but how exactly do we accomplish such a task? Well, recall the Sleppian Wolf encoder. Let Bob be the decoder and Alice be the transmitter of $X$.

If we assume that the Y encoder is perfect, then the Alice only needs to send at rate $H(X | Y)$ to convey $X$ to Bob. Now, to the outside observer, the rate $H(X | Y)$ is not possible for a noiseless reconstruction.

Concretely, recall that the SW encoder uses a hash function that pushes every $X^n$ into a bin $B$. Inside this bin, we give this $X^n$ an index $J$. So this $X^n$ can be described perfectly by $(B, J)$. To send this $X$ at the rate $H(X | Y)$, we only send the bin index $B$, as where are $2^{nH(X | Y)}$ of them.

On Bob’s side, the $B$ gives him the right bin to look at. Furthermore, he knows what $Y$ is. So from our previous discussion about Slepian-Wolf, we know that Bob can decode with high probability. So now bob has $X$ and alice has $X$. Both of them know the hash function, so it’s trivial to derive the $J$ part of the $X$ that wasn’t transmitted. Let $k = J$.

What is the entropy of $J$? Well, recall the grid of size $2^{nH(X)}$. It is uniformly distributed. So any slice is also uniform. The size of the slice is $2^{n(I(X; Y)}$. So the entropy is jut $nI(X; Y)$. This makes intuitive sense! We were able to transmit $nI(X; Y)$ bits of shared randomness.

Proof of optimality

So is this the best we can do? It turns out, Yes. Let’s proof it by using the converse. We will assert that $H(k) \leq nI(X; Y)$.

Let $k$ be the code that alice gets, and $k’$ be the code that bob gets. We have $k \approx k’$, so we have $H(k) \approx I(k; k’)$. Why? Well, $I(k; k’) = H(k) - H(k | k’) \approx H(k)$.

Now, let’s condition on the message. Because $I(k ; m) \approx 0$, we can say that $I(k; k’) \approx I(k; k’ | m)$

Now, we use something tricky. Recall that $X^n, Y^n$ are correlated. So we can construct the markov chain $k \leftarrow x^n — y^n → k’$. Note that both $m, y^n$ determine $k’$, but we already condition the MI on the $m$. By the data processing inequality we have $I(k; k’ | m) \leq I(X^n ; Y^n | m)$. We’re in the homestretch!

Let’s use the chain rule to yield $I(X^n ; Y^n | m) + I(m ; Y^n) = I(X^n, m ; Y^n)$. Given that $m$ is a deterministic function of $X^n$, we have $I(X^n, m; Y^n) = I(X^n; Y^n)$. Therefore, we have $I(X^n; Y^n | m) \leq I(X^n; Y^n)$.

To recap:

as desired.