Learning

• learn a model that captures the data distribution

• we can only approximate, because the data is often very high-dimensional

What can we learn?

• density estimators (energy functions)

• predictors

Learning from KL Divergence

We start from first principles of KL divergence to explain why log likelihood is sufficient

Derivation of Maximum Likelihood

So if we want to push $P_{data}$ close to $P_\theta$, we can use KL divergence to get the following:

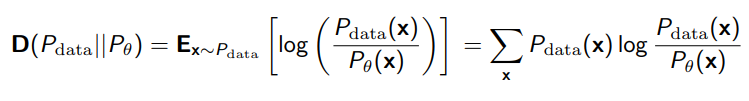
which we can simplify into

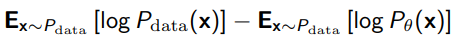
Note how the first term doesn’t depend on $\theta$, so the only thing that remains is the negative log-likelihood. This means that to minimize the KL divergence, it is sufficient to maximize the log likelihood!

Moving to empirical log-likelihood

Because we don’t know $P_{data}$, we can use a Monte Carlo sample

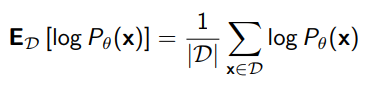
and we get

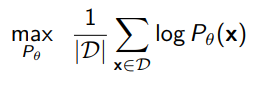
• recall that variance scales with $T$

Gradient Descent

The gradient of log-probability, as long as $p_\theta$ is differentiable, is well-defined. It isn’t convex, but it works well

Avoiding Overfitting

Regularize by model complexity, smaller networks, model sharing

Applying MLE

MLE can be used for any model with likelihood estimates, including autoregressive models

The relationship between L2, Likelihood, DKL ⭐

Sometimes, you want to do max-likelihood, and sometimes you want to do L2, etc. Is there a connection? Actually, yes!

So as you recall, this is a gaussian PDF:

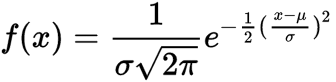
If you take the log-likelihood and set $\sigma = 1$, then you have recreated the L2 objective. You can imagine the $\sigma$ as modulating the importance of distance in L2 space. The larger the sigma, the less of a problem it is.

L2 losses also end up being equivalent to minimizing the KL divergence between the policy action distribution and the expert action distribution, as sampled under the expert action distribution (not the other way around).