Representing Models

Explicit

• composition of simple distributions in PGM format

• softmax (categorical)

• parameterize a simple distribution

• Sigmoid (for single distributions)

Implicit

• energy-based function (requires some special tools)

Classifier vs Generator

• Generator: you need to learn $p(x | z)$.

• Classifier: you need to learn $p(z | x)$

• Often it’s easier to learn a classifier. You can also make a classifier out of a generator, although you need to use Bayes rule

Training Models

Divergences

• Minimize the KL between data and generated distribution → reduces into maximum log likelihood objective

Surrogate Objective

• GAN → minimize JS divergence

• Energy-based models

We will talk about how these are used for each specific method

What you want in a model

Usually it’s easy to sample from a model than to evaluate it. In fact, some models can’t evaluate but they can sample.

• Evaluation
  • Is the model easy to evaluate the likelihood? This involves computing $p(x)$
    • potential difficulties: marginalization, lack of partition function, simply not learned
    • potential mitigations: Variational lower bound, contrastive (if ratios are easy to compute).

• Sampling
  • Is the model easy to sample from? This involves sampling from $p(x)$
    • Potential difficulties: lack of partition function
    • Potential mitigations: create objectives that don’t require model samples, use MCMC stochastic process

• Learning
  • Is the model easy to train?
    • Potential difficulties: issues with likelihood (see evaluation), high complexity
    • Potential mitigations: models-specific
  • Log-likelihood objectives are common. If you have latent variables, you need to use variational objective. You may also want to ditch log-likelihood for something more expressive (GAN). Or, it may simply not be computable (EBM)

• Latent
  • Does the model learn a latent representation of the data? Autoencoder-style objectives accomplish this

Autoregressive

For a lot of these deep models, we are trying to model a very complicated joint distribution. However, if there is good structure in your data, you can consider making a simple joint distribution that you can optimize using log-likelihood. It’s simple to optimize because there are no latent distribtuions.

This represents one type of model structure (structure, not learning method). Every output is conditioned on the past $p(x_1,…, x_n) = p(x_1) p(x_1|x_2)…p(x_n|x_{n-1},..., x_1)$

• Pros: very easy to sample and evaluate using maximum log-likelihood.

• Cons: you can’t do parallel generation

Types of autoregressive

• FVSBN: each conditional is $\sigma(\alpha_0 + \sum^{i-1}\alpha^i_jx_j)$

• NADE: Propagate a hidden vector autoregressively $h_i = \sigma(A_i x_{<i} + c_i)$, then simple output

• RNADE: same thing, but this time parameterize a mixture of gaussians

Autoregressive models act like masked autoencoders, masked such that there is conditional independence (otherwise, there isn’t such a good structure).

We add history to autoregressive models, but this doesn’t make life more difficult; we are still ultimately parameterizing a simple, computable, differentiable distribution.

Maximum Likelihood

Derived from KL objective and estimated with Monte Carlo

• apply gradient descent if you can take the grad-sum-log

• works for anything with likelihood estimates

VAE

You want to parameterize $p(x , z)$, but you want to do MLE on just $x$. What do you do?

• Turn the sum over $z$ into an expectation using an importance weight

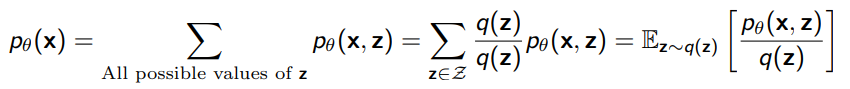
Now, from Jensen’s inequality, we can lower-bound the log-prob as

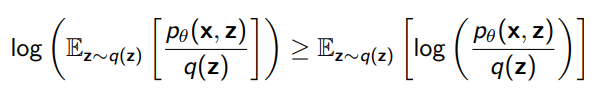
And this gets you a differentiable method to compute the log-prob of $p(x)$, which can be used for optimization.

Note that any $q$ works, although some works better (tight when $q(z) = p(z | x)$, an intractable value.

Further analysis

If you start from the KL divergence, you get a different identity that outlines the tightness of the bound

Practical Stuff

Generator gradient: propagate through expectation, use Monte Carlo estimate of samples from $q$ to get

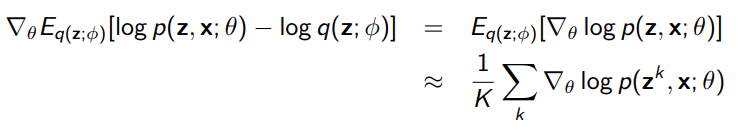
Note that you need some notion of the prior, i.e. you might factor $p(x, z) = p(x | z)p(z)$. This is the most common approach.

Posterior gradient: use reparameterization trick on a distribution that can be shifted and scaled

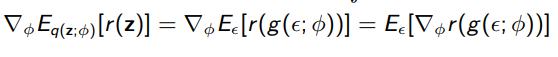
We usually amortize the $q$ by making it a function of $x$, i.e. $q(z | x)$.

Autoencoder interpretation

You can rearrange the ELBO into a reconstruction objective and a KL regularizer

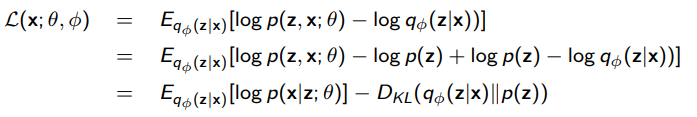
which shows us that this is just a regularized autoencoder! This is typically the objective that you use. It also shows us that if we aren’t careful, we may deal with posterior collapse, where we learn to ignore $z$.

PROS AND CONS

• Simple computation of gradient (easy to train)

• Relatively stable method

• Hard to evaluate likelihood (whole setup built around avoiding likelihood)

• Easy generation (sample from prior, compute $x$).

• Creation of a latent representation

Normalizing Flow

Instead of computing $p(x | z)$, we can compute some invertible mapping. We have a complicated $x$ and a simple $z$. We can map from $z$ to $x$ through $f$ (sampling) and $x$ to $z$ through $f^{-1}$ (evaluation).

You can train a normalizing flow directly through a maximum likelihood objective

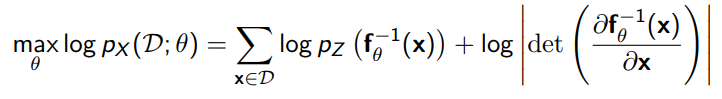
The problem is often computing the determinant. We want a determinant that can be computed quickly. Often, this takes place in triangular matrices (product of the diagonal)

NICE

The idea here is to create the $f$ such that the inverse is very easy to compute. We do this by changing only one half of the variables

• $x_{1:d} = z_{1:d}$

• $x_{d+1:n} = z_{d+1:n} + m_\theta(z_{1:d})$, where $m_\theta$ is any arbitrary function

The jacobian is therefore easily defined

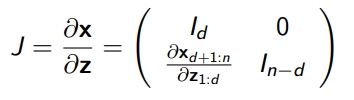
and this evaluates to 1. If we do arbitrary partitions and compose the $f$ together, we have good mixing.

Real NVP

We make a simple modification: we also scale one of the components by a function

• $x_{1:d} = z_{1:d}$

• $x_{d+1:n} = z_{d+1:n} \odot\exp(\alpha_\theta(z_{1:d}))+ \mu_\theta(z_{1:d})$, where we have two neural networks.

which also yields a jacobian that is quite easy to compute

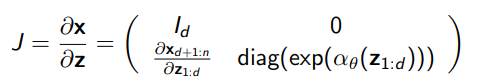
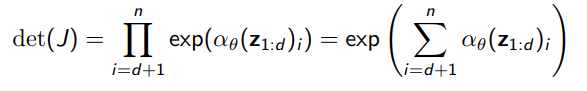
Autoregression and flow

If you had an autoregressive model that outputted parameterized gaussians, the reparameterization trick will tell us that you’re actually computing the flow from a set of $n$ IID gaussians to the $x$ output space. The creation is autoregressive, so it makes each of these independent noise elements become entangled

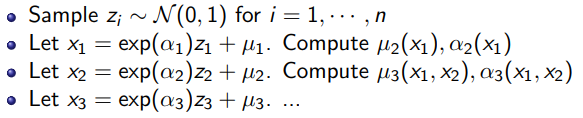
To map from $z→x$ is slow because autoregressive. On the other hand, with all $x$, you can easily compute all $z$’s, which perhaps helps with training.

You can speed up the sampling process by inverting the sampling process. What if we made the autoregressive computation happen on the $z$’s? By using the sliding window, we still get the autoregressive dependence structure in $x$. However, because we know all the $z$’s ahead of time, we can compute the weights in parallel

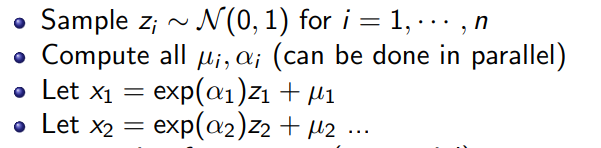
Intuitively, this works because of the data processing inequality: if we generated all $x$ from the $z$, then the $z$’s give us more information than the $x$’s, so it’s fine to keep on using the $z$’s (instead of the $x$’s) to generate more $x$’s.

Of course, no free lunch: the inverse mapping is now autoregressive.

Note: there’s nothing special about using the gaussian, other than the interpretation of means and variances. We can use any distribution.

Other normalizing flow models

• Mintnet: masked convolutions apply flow models to images

• Gaussianization flows: a method to turn data into gaussians through invariance property

PROS AND CONS

• direct computation of likelihoods (no lower bound)

• possible to create pretty expressive functions

• You don’t really learn a “latent” variable (because it’s the same dimension)

• You can’t condense information

GAN

All the models so far have been optimizing a maximum likelihood objective (i.e. the model should rank data as high likelihood). What if we start to consider different divergences?

• maximum likelihood may be too weak of an objective for good generation

• conversely, high maximum likelihood could indicate overfitting and not a good generation

To do this, we just do a min-max game between a generator and a discriminator

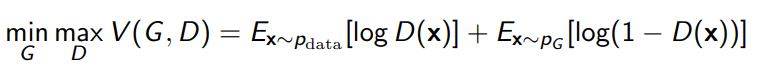
The optimal discriminator will satisfy

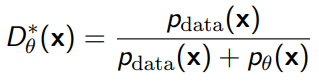
The proof comes from calculus. Ultimately, if this optimal discriminator is reached, the outer objective can be rewritten as the JS divergence, which mean that the GAN is secretly optimizing a different divergence.

However, this is only a theoretical guarantee. In reality, we can’t reach this optimal discriminator, so we just do two gradient operations at once

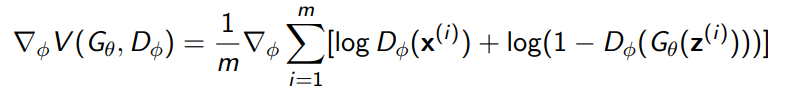
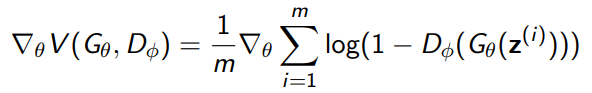
f-GAN

We can generalize the GAN objective such that there exists a GAN for every $f$ divergence. Turns out, we can derive (see real notes) as lower bound for the divergence.

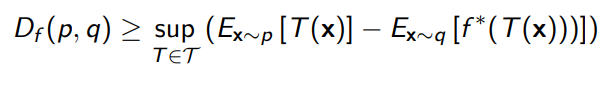
which means that you can construct a GAN objective

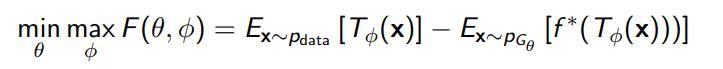
where $f^*$ is the fenchel conjugate. Intuitively, the inner objective makes the lower bound close to the true objective, and the outer objective minimizes this true objective. Of course, we might not get there, and that’s fine. It’s simialr to VAE, where you might optimizing a slightly different objective.

Wasserstein GAN

The Wasserstein distance is defined as

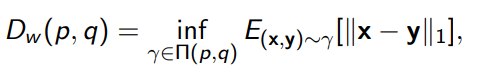
And it’s often a smoother distance function between $p, q$. We can create a similar GAN objective

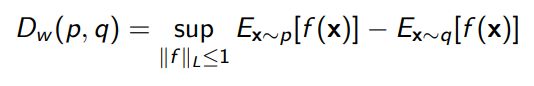
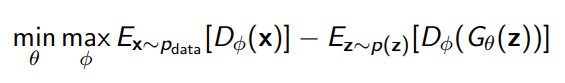
And in fact, it looks suspiciously like the vanilla GAN. Indeed, the only difference is that we need to keep the lipshitz property of the discriminator by clipping the weights.

Making Latent representations

We can make latent representation by making an explicit objective that encodes the data.

In general, we can start to have different domains that we transfer between

PROS AND CONS

• con: can mode collapse (if it finds a really good generation, it could just keep on using that)

• Con: sensitive in general

• Con: oscillating loss, no sopping criteria

• Pro: the GAN game can create pretty convincing outputs sometimes

Energy Models

In all previous setups, we had to model an explicit probability distribution. We did this by parameterizing a distribution, or using a categorical distribution. However, this can be limiting. We we implicitly learn through an energy function?

We define the energy-based model as $f$, where

Contrastive Divergence

We can try to directly optimize the likelihood, which gets us this objective

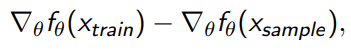
Intuitively, we’re trying to maximize the likelihood of the data and contrast this with the model’s own performance.

Sampling

To sample from EBM, you need to use MCMC, which is essentially taking noisy steps towards higher likelihoods. You can also compute directly the score function of an EBM, which allows you to do Langevin MCMC.

Score Matching

Instead of using contrastive divergence, we can just take the Fisher Divergence between the score of the data and the score of the model.

After a derivation, you can get that

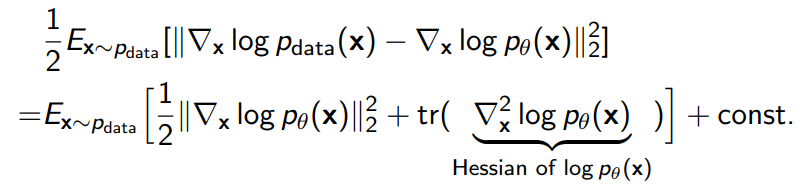
which allows you to optimize without needing the gradient of the data score. More importantly, this allows you to optimize the model without sampling from it.

Noise Contrastive Estimation

Here, you can frame the EBM as a noise discrimination problem, and if you parameterize the $D$ in special way, you will implicitly train the EBM and the partition function. This all depends on the data samples, not the EBM samples. We can make this better by creating a better baseline for contrastive learning (which can be learned adversarilly)

Variational Paradigm

We can also estimate the lower bound of the log likelihood and get a VAE paradigm

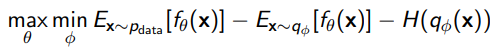
PROS AND CONS

• Hard to find likelihood (or even estimate a likelihood)
  • Workaround for training: use a sampling-based approach

• Easy to compute relative rankings of things (good classifier)

• Can’t directly sample (must use MCMC)
  • Workaround: use score matching