Autoregressive models

We can potentially factor a distribution autoregressively: $p(x_1,…, x_n) = p(x_1) p(x_1|x_2)…p(x_n|x_{n-1},..., x_1)$

Autoregressive models are quite easy to sample from (they are already topologically sorted). It is also easy to compute their likelihoods.

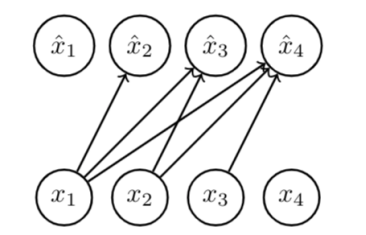
FVSBN

We can apply this autogressive paradigm to make the fully visible sigmoid belief network (FVSBN)

Now, you can model each conditional distribution as the logistic regression

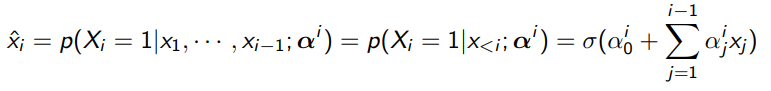
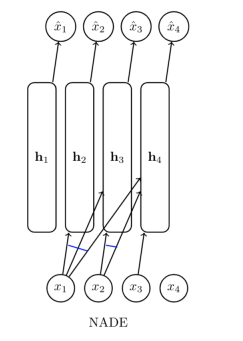
NADE

We can make things more complicated by using a neural autoregressive density estimation, which means that you add a neural network layer before the logistic regression

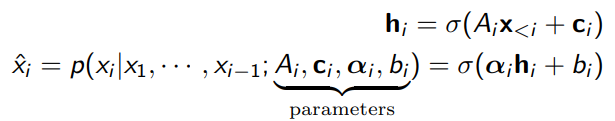
For a categorical distribution, use the softmax. The softmax is a generalization of the sigmoid.

RNADE

Same as NADE, but this time, $\hat{x}$ is the parameters to a mixture of gaussians

The autoencoder interpretation

You can think about the autoregressive model as being a masked autoencoder. It takes in things from the past, compresses it, and uses it to predict the future. We mask the encoder because we don’t want to learn an identity mapping.

So, can we just use a normal autoencoder to do the things we saw above? Well, a normal autoencoder doesn’t have structure, i.e. everything is interdependent

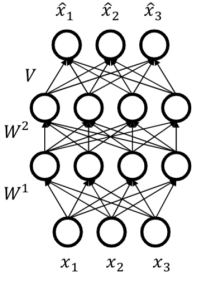
By adding masks, we force the autoencoder to adopt some structure in generation

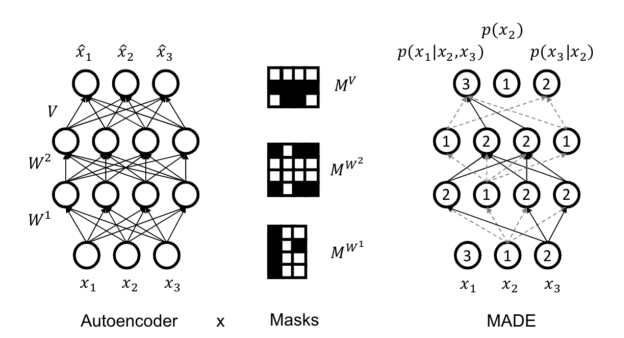
If we disallow certain paths, it’s as if we are making them independent from each other. This means that we can use the autoencoder autoregressively. Think about it as running the autoencoder $n$ times, with $n$ being the number of variables.

Better History encoding

So far, we’ve just added more history as inputs to our function. This can become cumbersome, which is why newer models deal with history in a smarter way. Notably, RNNs and transformers use mechanisms to keep the memory short.