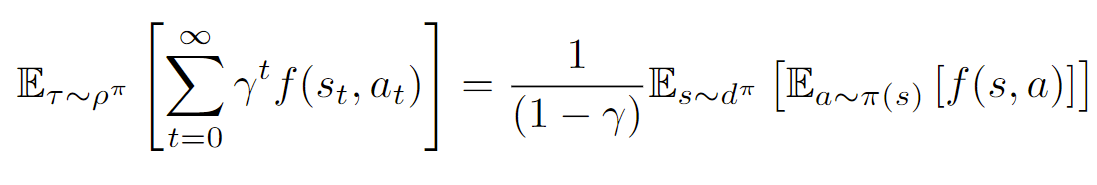Trajectory distributions $p(\tau)$

As shown in the previous section, there is the concept of a trajectory distribution, which is literally the distribution of a rollout tuple $(s_0, a_0, s_1, a_1,…)$. With the dynamics and the policy, it is a directed bayesian model with factorization

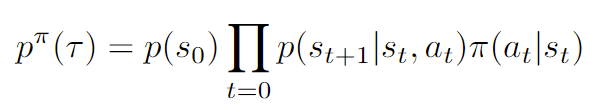
represented typically by $p(\tau)$. This is just a factorization using the chain rule and the MDP. Note that $p(\tau)$ is dependent on $\theta$.

State marginals

We can marginalize out all the states except for one to get $p(s_t = s)$. Because this is a factorable graph, we can use the variable elimination algorithm and complete it in polynomial time.

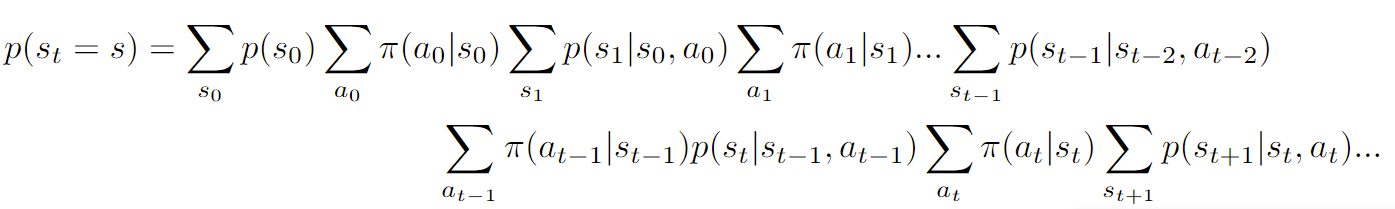
State marginals are stationary in infinite horizon

We can also arrive at the state marginals under the knowledge that for an MDP, the state marginal is the stationary distribution as $t → \infty$. Same with state-action marginals.

Discounted Stationary Distribution

We can define the discounted state distribution as the following:

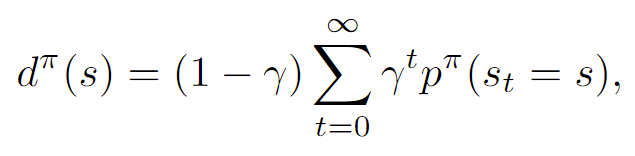
At first this seems a little weird, but intuitively, it weighs the state likelihoods by how late they show up (i.e. how much we should care). We care about this because it shows up in quite a few expressions.

We can also write this recursively:

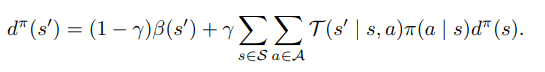
where $\beta$ is the starting distribution. This should look suspiciously like a value function recursion, which brings us to why we even use a discounted stationary distribution

Why care about Discounted Stationary distribution?

Actually, there’s a pretty neat identity that is useful. So if we let

then $E[V(s_0)] = R^T\chi$, where $R$ is the vector of all rewards for $(s, a)$. Think about this for a second. By the definition of $d^\pi$, it should be apparent where it comes from.

Stationary Distribution Identity ⭐🚀

This following identity essentially shows a relationship between an expectation across trajectories to an expectation across discounted stationary distributions

• Proof (linearity of expectation, marginalization)